[BOJ] 백준 1766번 : 문제집 (JAVA)
문제
민오는 1번부터 N번까지 총 N개의 문제로 되어 있는 문제집을 풀려고 한다. 문제는 난이도 순서로 출제되어 있다. 즉 1번 문제가 가장 쉬운 문제이고 N번 문제가 가장 어려운 문제가 된다.
어떤 문제부터 풀까 고민하면서 문제를 훑어보던 민오는, 몇몇 문제들 사이에는 '먼저 푸는 것이 좋은 문제'가 있다는 것을 알게 되었다. 예를 들어 1번 문제를 풀고 나면 4번 문제가 쉽게 풀린다거나 하는 식이다. 민오는 다음의 세 가지 조건에 따라 문제를 풀 순서를 정하기로 하였다.
1. N개의 문제는 모두 풀어야 한다.
2. 먼저 푸는 것이 좋은 문제가 있는 문제는, 먼저 푸는 것이 좋은 문제를 반드시 먼저 풀어야 한다.
3. 가능하면 쉬운 문제부터 풀어야 한다.
예를 들어서 네 개의 문제가 있다고 하자. 4번 문제는 2번 문제보다 먼저 푸는 것이 좋고, 3번 문제는 1번 문제보다 먼저 푸는 것이 좋다고 하자. 만일 4-3-2-1의 순서로 문제를 풀게 되면 조건 1과 조건 2를 만족한다. 하지만 조건 3을 만족하지 않는다. 4보다 3을 충분히 먼저 풀 수 있기 때문이다. 따라서 조건 3을 만족하는 문제를 풀 순서는 3-1-4-2가 된다.
문제의 개수와 먼저 푸는 것이 좋은 문제에 대한 정보가 주어졌을 때, 주어진 조건을 만족하면서 민오가 풀 문제의 순서를 결정해 주는 프로그램을 작성하시오.
입력
첫째 줄에 문제의 수 N(1 ≤ N ≤ 32,000)과 먼저 푸는 것이 좋은 문제에 대한 정보의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에 걸쳐 두 정수의 순서쌍 A,B가 빈칸을 사이에 두고 주어진다. 이는 A번 문제는 B번 문제보다 먼저 푸는 것이 좋다는 의미이다.
항상 문제를 모두 풀 수 있는 경우만 입력으로 주어진다.
출력
첫째 줄에 문제 번호를 나타내는 1 이상 N 이하의 정수들을 민오가 풀어야 하는 순서대로 빈칸을 사이에 두고 출력한다.
풀이
위상정렬과 우선순위 큐를 활용한 문제였습니다. 위상정렬에 대한 개념을 모르시는 분은 아래 포스팅을 읽고 오시길 바랍니다.
위상정렬 Topological Sort (Java)
위상정렬 연습 문제 1 연습 문제 2 위상 정렬은 그래프 정렬을 말합니다. 그래프의 순서를 정렬하기 때문에 조건이 있습니다. 위상 정렬이 가능하려면 DAG(Directed Acyclic Graph, 방향성이 있으며 사��
bcp0109.tistory.com
이 문제의 핵심은 먼저 풀어야하는 문제와 나중에 풀어야하는 문제를 분류하는 것이었습니다. 그리고 이 과정에서 위상정렬을 사용하면 쉽게 해결할 수 있었습니다.
방식은 간단합니다. 특정 문제에 대하여 먼저 풀어야하는 문제의 개수를 indegree라는 배열을 정의하여 값을 넣어주면 됩니다. 예를 들어, 2번 문제보다 3, 5번 문제를 먼저 풀어야 한다면, indegree[2] = 2로 초기화하는 식입니다.
위와 같은 방식으로 indegree 배열에 값을 적절히 넣어준 후, indegree[i] = 0인 i를 우선순위 큐에 offer합니다. 우선순위 큐를 사용하는 이유는 가능하면 쉬운 문제부터 풀어야한다는 조건이 있었기때문입니다.
그리고 우선순위 큐를 poll하면서 값(now)을 출력하고, now보다 나중에 풀어야하는 문제(next)가 있는지 판단합니다.
만약, now보다 나중에 풀어야하는 문제가 존재한다면, indegree[next]--를 합니다. 그리고 indegree[next]가 0이라면, 더이상 next보다 먼저 풀어야하는 문제가 없기때문에 우선순위 큐에 offer합니다.
now와 next를 판단하는 과정은 우선순위 큐가 Empty인 상태까지 반복하면 됩니다.
아래 예시를 통해서 확실히 이해를 해 봅시다.
예시
N = 5, M = 2
1 - { }
2 - { }
3 - { }
4 - {2, 3}
5 - {3}
( { }는 특정 문제보다 나중에 풀어야하는 문제가 없음을 의미합니다. )
위의 예시를 도식화해 보면 아래와 같습니다.
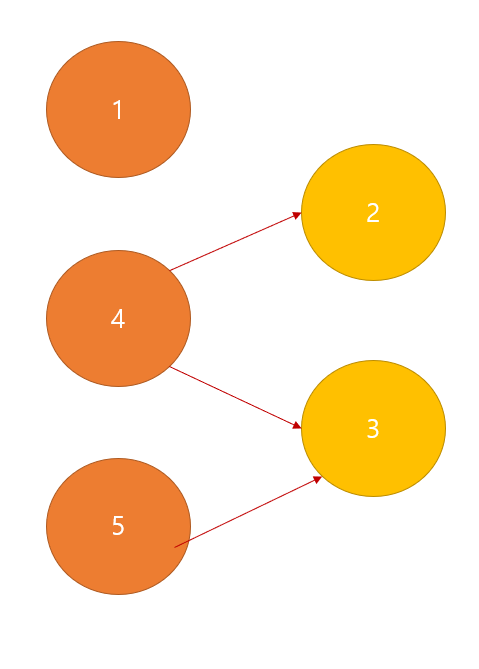
indegree[2] = 1, indegree[3] = 2이고, indegree[1] = indegree[4] = indegree[5] = 0인 상황입니다.
먼저, 우선순위 큐에 1, 4, 5를 offer하고 순서대로 poll를 합니다.
1과 연결된 문제는 없으므로 1을 출력만 하고 우선순위 큐에서 다음 요소를 가져옵니다.
4와 연결된 문제는 2와 3이 있습니다. 먼저, indegree[2] = 1인 상황인데, 4번 문제를 풀었으므로 indegree[2]--을 취합니다. 이 때, indegree[2] = 0이 되므로 다시 우선순위 큐에 offer합니다.
마찬가지로, indegree[3] = 2인 상황인데, 4번 문제를 풀었으므로 indegree[3]--을 취합니다. indegree[3]은 0이 아니므로 우선순위 큐에 offer를 하지는 않습니다.
5와 연결된 문제는 3이 있습니다. indegree[3] = 1인 상황인데, 5번 문제를 풀었으므로 indegree[3]--을 취합니다. 이 때, indegree[3] = 0이 되므로 우선순위 큐에 offer 합니다.
현재, 우선순위 큐에는 2와 3이 들어가 있는 상태입니다.
2와 3은 각각 연결된 문제가 없으므로 단순히 poll을 한 후, 출력만 하면 됩니다.
따라서 정답은 1 - 4 - 5 - 2 - 3이 된다는 사실을 알 수 있습니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[] indegree = new int[N + 1];
ArrayList<ArrayList<Integer>> a = new ArrayList<>();
for (int i = 0; i <= N; i++) {
a.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int first = Integer.parseInt(st.nextToken());
int last = Integer.parseInt(st.nextToken());
a.get(first).add(last);
indegree[last]++; // 특정 문제의 번호보다 먼저 풀어야하는 문제의 개수
}
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 1; i <= N; i++) {
if (indegree[i] == 0) { // 먼저 풀어야하는 문제가 없는 경우
pq.offer(i);
}
}
StringBuilder sb = new StringBuilder();
while (!pq.isEmpty()) {
int now = pq.poll();
sb.append(now + " ");
// now와 연결된 문제가 있는지 확인.
for (int next : a.get(now)) {
// now에 해당하는 문제를 풀었기때문에
// next보다 먼저 풀어야하는 문제의 개수가 1개 줄어듦.
indegree[next]--;
// 먼저 풀어야하는 문제가 없는 경우
// 새롭게 큐에 데이터를 집어넣는다.
if (indegree[next] == 0) {
pq.offer(next);
}
}
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
}
|
cs |
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 2623번 : 음악프로그램 (JAVA) (0) | 2020.07.21 |
|---|---|
| [BOJ] 백준 1516번 : 게임 개발 (JAVA) (0) | 2020.07.20 |
| [BOJ] 백준 1916번 : 최소비용 구하기 (JAVA) (2) | 2020.07.17 |
| [BOJ] 백준 18119번 : 단어 암기 (JAVA) (0) | 2020.07.15 |
| [BOJ] 백준 1504번 : 특정한 최단 경로 (JAVA) (4) | 2020.07.14 |



댓글