[BOJ] 백준 11266번 : 단절점 (JAVA)
문제
그래프가 주어졌을 때, 단절점을 모두 구해 출력하는 프로그램을 작성하시오.
단절점이란 그 정점을 제거했을 때, 그래프가 두 개 또는 그 이상으로 나누어지는 정점을 말한다. 즉, 제거했을 때 그래프의 connected component의 개수가 증가하는 정점을 말한다.
입력
첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다.
다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이며, 방향은 양방향이다.
입력으로 주어지는 그래프는 연결 그래프가 아닐 수도 있다.
출력
첫째 줄에 단절점의 개수를 출력한다.
둘째 줄에는 단절점의 번호를 공백으로 구분해 오름차순으로 출력한다.
풀이
DFS를 응용하여 풀 수 있는 문제였습니다.
먼저, 문제의 예시를 통해서 단절점이 무엇이고, 어떤 정점이 단절점인지 알아보겠습니다.
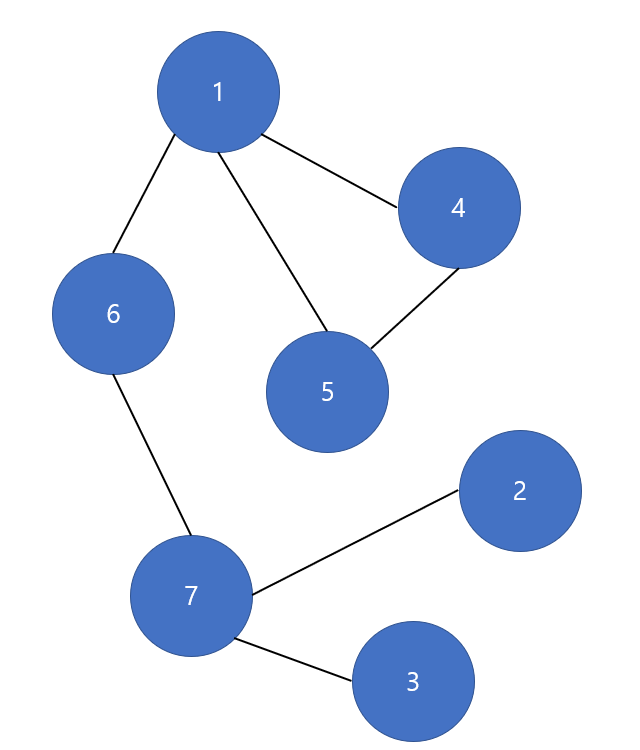
정점의 연결 관계를 나타내면 위와 같습니다.
단절점에 해당하는 정점을 구하기 전에 단절점이 무엇인지 알아봅시다.
단절점은 해당 정점을 지웠을 때, 하나의 연결 그래프가 둘로 나뉘는 점을 말합니다.
가령, 위 그래프에서 1번 정점을 없앴다면, 아래 그림과 같이 (4, 5), (2, 3, 6, 7) 로 연결 그래프가 나뉘게 될 것입니다.

그렇다면, 1번 정점이 아니라 한 번 다른 정점을 지워봅시다.
예를 들어, 2번 정점을 지워 보겠습니다.

단순히 정점 1개만 줄어들었을 뿐, 연결그래프는 여전히 1개이므로 2번 정점은 단절점이 아닙니다.
이와 같이 1번부터 7번까지 모두 지워보면서 단절점을 파악해보면, 아래 주황색으로 색칠한 정점인 1, 6, 7번이 단절점에 해당합니다.

이 문제를 풀기 위해서 가장 처음 생각해 볼 부분은 브루트 포스입니다.
정점을 1개씩 지워보고, 모든 정점의 연결 그래프 개수가 원래와 일정한지 따져보는 것이죠.
하지만, V의 최대 범위 10,000이고, E의 최대 범위는 100,000 이라서 시간 초과를 피할 수 없습니다.
따라서, 좀 더 효율적인 방식을 찾아야 합니다.
그러기 위해서는 일단 단절점이 갖는 특징을 한 번 살펴봐야 합니다.
먼저, 단절점은 빨간색, 단절점과 연결된 간선은 연두색으로 색칠해 보겠습니다.
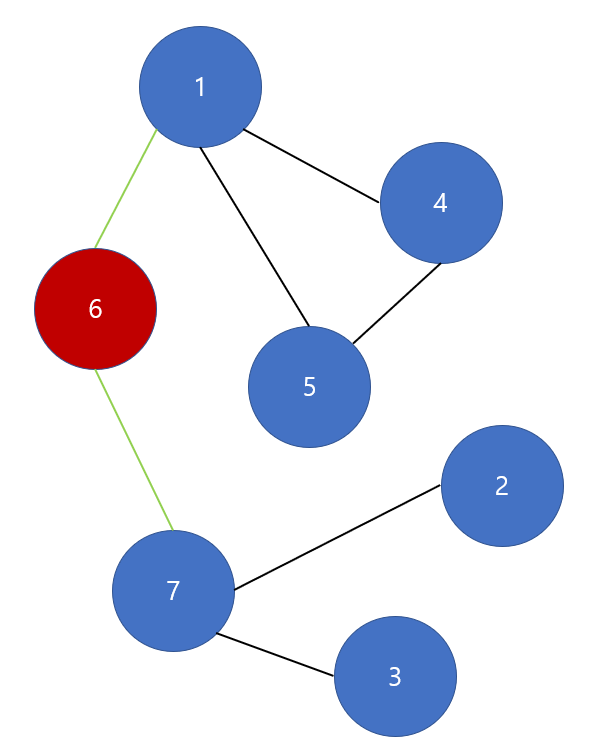
단절점 6번과 연결된 정점은 1번과 7번 정점입니다.
그리고 1번과 7번 정점은 6번 정점을 거치지 않고서는 서로 방문할 수가 없습니다.
따라서, 어떤 A번 정점과 연결된 모든 정점이 A번 정점을 거치지 않고 갈 수 있는 우회 경로가 없다면, A번 정점은 단절점입니다.
이것을 알기 위해서는 각 정점 별로 방문 순서를 붙이는 것이 편합니다.
각 정점에 대해서 방문 순서는 DFS에 따라 정의됩니다. 단, 정점이 작은 정점을 더 우선적으로 탐색하겠습니다.
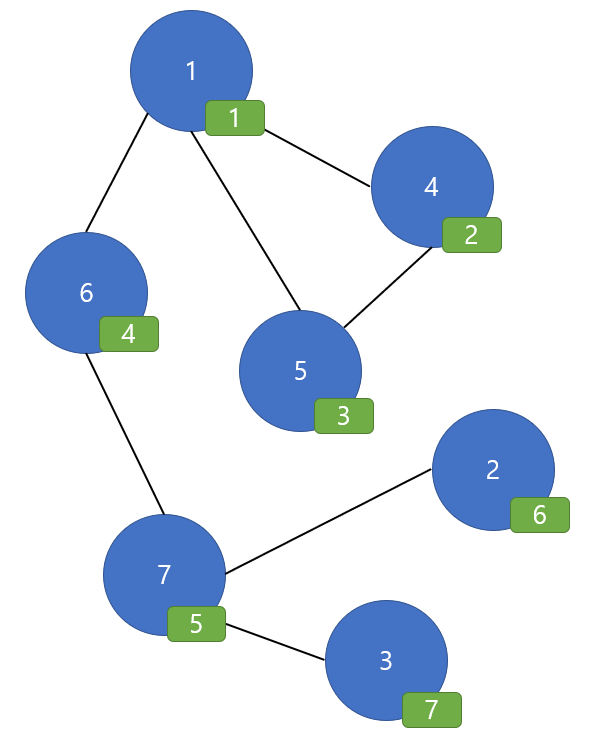
위와 같이 초록색 직사각형 부분에 방문 순서를 적어 두었습니다.
이제, 위에서 6번 단절점에 대해서 다시 보겠습니다.

6번과 인접한 정점은 1번과 7번 정점이 있습니다. 이 때, 7번 정점은 (1, 4, 5)번 정점에 방문할 수 없습니다.
여기서 1번 정점을 고려하지 않은 이유는, 이미 1번 정점은 방문 순서가 확정되었기 떄문입니다.
즉, 특정 A번 정점의 방문 순서보다 방문 순서가 늦은 자식 정점이 우회 경로를 거쳐서 A번 방문 순서보다 더 빠른 정점에 도달할 수 없으면 그 점은 단절점이 됩니다.
이것을 이용하여 DFS를 통해 탐색되는 순서대로 방문 순서를 매겨 주되, 아직 탐색이 안 된 정점(now)에 경우, 해당 정점에서 DFS를 통해 탐색하여 나오는 정점 중 방문 순서가 가장 빠른 정점(low)을 찾습니다.
이 때, low의 방문 순서가 now의 방문 순서보다 크거나 같다면, now는 단절점이 되는 것입니다.
6번 정점의 경우 low가 4가 되므로 now와 low의 방문 순서가 서로 같게 되어 6번 정점은 단절점입니다.
위와 같은 로직으로 문제를 풀면, 한 가지 예외 상황이 발생합니다.
바로, 정점이 루트일 경우죠.
1번 정점의 경우 방문 순서가 1번이고, 이것보다 빠른 방문 순서는 존재하지 않습니다.
만약, 1번 정점 하나만 존재하거나, 자식 정점이 1개만 존재한다면, 1번 정점을 지워도 연결 그래프는 1개를 유지하게 됩니다.
따라서, 이 경우는 자식 정점이 2개 이상일 때만 단절점이라는 것에 유의하셔야 합니다.
아래 소스코드에 주석을 찬찬히 읽어보면서 이해해 보시길 바랍니다.
소스코드
주의할 점
74번째 줄부터 자식 검사를 시작하는데, A번 정점보다 방문 순서가 빠른 정점도 for문을 통해 비교를 한다는 것을 알 수 있습니다.
여기서, 저는 "어? 그러면 low는 A번 정점보다 빠른 방문 순서가 될 수 있지 않을까?" 라는 생각을 했습니다.
예를 들어, 6번 정점에 경우 1번과 7번 정점을 탐색하는데, 1번 정점은 가장 빠른 방문 순서인 1이니까
low = 1이 되지 않을까라는 오해를 한 것입니다.
코드를 자세히 보면 알 수 있듯이, if~else 구문에서 1번 정점은 이미 방문했으므로 dfs를 통해 탐색을 하지 않는다는 사실을 알 수 있습니다.
따라서, 6번 정점이 1번 정점으로 갈 수 있다는 이야기지, 6번의 자식 정점의 방문 순서 중 가장 빠른 방문 순서는 4가 될 수 밖에 없다는 점을 주의하셔야 합니다.
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 1735번 : 분수 합 (JAVA) (2) | 2020.11.10 |
|---|---|
| [BOJ] 백준 11000번 : 강의실 배정 (JAVA) (7) | 2020.11.09 |
| [BOJ] 백준 1339번 : 단어 수학 (JAVA) (2) | 2020.11.05 |
| [BOJ] 백준 14698번 : 전생했더니 슬라임 연구자였던 건에 대하여 (Hard) (JAVA) (6) | 2020.11.03 |
| [BOJ] 백준 14715번 : 전생했더니 슬라임 연구자였던 건에 대하여 (Easy) (JAVA) (2) | 2020.11.02 |



댓글