[BOJ] 백준 14715번 : 전생했더니 슬라임 연구자였던 건에 대하여 (Easy) (JAVA)
문제
안녕? 내 이름은 ntopia!
나는 원래 지구에 살고 있던 평범한 20대 청년이었어. 어느 날 길을 걷다가 괴한의 칼에 찔려 죽어버렸어. 그런데 이게 무슨 일이람! 정신을 차려보니 이세계에 떨어져 버렸지 뭐야. 여기에서 나는 슬라임을 전문으로 연구하는 슬라임 연구자가 되어버린 것 같아.
나는 지금 아주 중요한 연구를 진행하고 있어. 이 연구가 성공하면 나는 내가 살던 세계로 돌아갈 수 있게 될 거야. 이 연구를 도와주지 않겠니?
이곳의 슬라임은 모두 슬라임 에너지라는 것을 갖고 있고 그 양은 2 이상의 자연수로 표현돼. 나는 슬라임을 분할했을 때 슬라임 에너지가 어떻게 변화하는지에 대해 연구하고 있어.
슬라임 분할 과정은 1마리를 분할해서 2마리를 만들어내는 식으로 이루어져. K만큼의 슬라임 에너지를 가진 슬라임이 있었다고 해보자.
이 슬라임을 적절히 분할하면 A만큼의 에너지를 갖는 슬라임과 B만큼의 에너지를 갖는 슬라임을 만들 수 있고 (A, B는 2 이상의 자연수), 항상 K = A × B 를 만족해. 이렇게 분할하다보면 언젠가는 분할이 되지 않는 슬라임도 생기겠지?
그리고 슬라임 분할 기술이 아직 완벽하지 않아서 슬라임을 분할할 때마다 흠집이 하나씩 생기게 돼. 구체적으로, 흠집이 T개인 슬라임을 분할하면 흠집이 T + 1개인 슬라임 2마리가 생기는 것이지.

에너지가 24이고 흠집이 1개인 슬라임을 분할한 모습. 에너지가 4이고 흠집이 2개인 슬라임과 에너지가 6이고 흠집이 2개인 슬라임으로 분할되었다.
나에겐 지금 슬라임 에너지가 K이고 흠집이 하나도 없는 슬라임이 있어. 이 슬라임을 분할하고 또 분할해서 분할이 가능한 슬라임이 존재하지 않을 때까지 마구마구 분할해야해.
그렇게 다 분할하고나면 마지막에 남은 슬라임들에 흠집이 적당히 생겼겠지? (물론 생기지 않았을 수도 있어) 그 슬라임들 중에서 흠집이 제일 많이 생긴 녀석의 흠집 개수가 최소가 되도록 분할을 적절히 수행하는 것이 내 연구의 목표야.
내 연구를 도와줘! 부탁이야!!
입력
첫 번째 줄에 처음 주어진 슬라임의 에너지 K (2 ≤ K ≤ 1, 000, 000) 가 주어진다.
출력
슬라임을 끝까지 분할했을 때, 가장 많이 생긴 흠집의 개수의 최솟값을 출력한다.
풀이
소인수 분해를 활용하여 풀 수 있는 문제였습니다.
문제에서는 특정 수 K에 대하여 A X B = K (A, B는 2 이상) 를 만족하는 A와 B로 더 이상 나눌 수 없을 때까지 나누라고 하였습니다.
따라서, 소인수 분해를 통하여 K = p1q1 + p2q2 + p3q3 + ... 로 나타낼 수 있습니다.
이 때, 슬라임들에게 흠집을 최소한으로 남기려면 완전이진트리를 만족해야 합니다.
여기서, 완전 이진 트리란 마지막 레벨을 제외한 모든 레벨의 node가 완전히 채워져 있으며, 마지막 레벨의 node들은 가능한 한 왼쪽부터 채워져 있는 구조를 말합니다.
즉, 소인수 분해를 할 때, 트리의 형태가 완전이진트리가 되도록 나누고, 그 트리의 높이를 구하면 됩니다.
K = 24일 때를 예로 들겠습니다.
24를 가장 기본적인 방식으로 소인수 분해를 하면 아래와 같습니다.
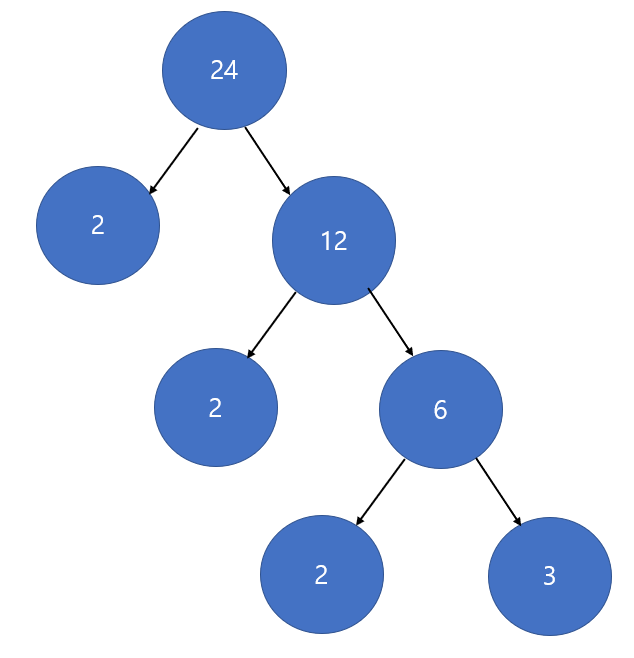
단순히 2씩 나누면서 트리를 형성하면 위와 같고, 트리의 높이는 3이 됩니다.
하지만, 이것은 최소 높이가 되지 않습니다.
이와 달리, 완전 이진 트리를 만족하게끔 나누어보겠습니다.

이렇게 하면, 높이가 2로 아까보다 작아짐을 알 수 있다는 것을 알 수 있습니다.
그렇다면, 완전이진트리의 높이는 어떻게 구할 수 있을까요?
완전이진트리는 0 레벨에서 노드가 1개, 1 레벨에서 노드가 2개, 2 레벨에서 노드가 4개로, 2의 거듭제곱 형태로 노드가 늘어납니다.
24를 소인수 분해하였을 때, 2가 3개, 3이 1개가 나오는데 이것은 모두 자식 노드가 없는 리프 노드에 해당합니다.
따라서, 리프 노드의 개수를 전부 더하고 그 값에 log2를 씌우면 마지막 층에 레벨을 구할 수 있게 되고, 그것이 바로 트리의 높이가 됩니다.
식으로는 log2(q1 + q2 + q3 + ... ) 이 되겠습니다.
단, 위에서 구한 값이 정수로 딱 떨어지지않는다면, 올림을 취해 주어야 합니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 1339번 : 단어 수학 (JAVA) (2) | 2020.11.05 |
|---|---|
| [BOJ] 백준 14698번 : 전생했더니 슬라임 연구자였던 건에 대하여 (Hard) (JAVA) (6) | 2020.11.03 |
| [BOJ] 백준 1758번 : 알바생 강호 (JAVA) (0) | 2020.11.02 |
| [BOJ] 백준 9732번 : Division Game (JAVA) (4) | 2020.10.29 |
| [BOJ] 백준 9095번 : 1, 2, 3 더하기 (JAVA) (0) | 2020.10.26 |



댓글