[BOJ] 백준 6549번 : 히스토그램에서 가장 큰 직사각형 (JAVA)
문제
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.

히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
풀이
세그먼트 트리와 분할 정복을 이용하여 풀 수 있는 문제였습니다.
저는 이전까지 단순히 구간 합이나 곱, 최솟값, 최댓값을 구하기 위하여 세그먼트 트리를 이용하였지만, 이번 문제에서는 도대체 무엇을 기준으로 세그먼트 트리를 구성해야하는지 파악할 수가 없었습니다.
결국, 아래 블로그 포스팅에서 힌트를 얻은 후 문제를 풀어낼 수 있었습니다.
[6549번] 히스토그램에서 가장 큰 직사각형
문제 출처 : https://www.acmicpc.net/problem/6549 알고리즘 분석 : 문제 해결에 필요한 사항 1. 세그먼트 트리(Segment Tree) :: http://www.crocus.co.kr/648 세그먼트 트리를 이용하여 O(nlgn)에 해결 할 수..
www.crocus.co.kr
위의 풀이를 조금 더 덧붙여서 설명하는 방향으로 글을 작성하겠습니다.
먼저, 전반적인 로직은 다음과 같습니다.
1. 세그먼트 트리의 리프 노드는 arr의 인덱스를 차례대로 넣는다. (arr은 직사각형의 높이 배열을 의미)
2. 리프 노드를 제외한 나머지 노드는 그 아래 노드 중 직사각형의 높이가 작은 인덱스로 채워 넣는다.
3. [1, N] 구간에서 이분 재귀 탐색을 수행한다.
1번 과정부터 차례 차례 설명해 드리겠습니다.
문제의 예시를 통해서 세그먼트 트리를 구현하겠습니다.
arr = { 2, 1, 4, 5, 1, 3, 3 } -> 직사각형의 높이
처음에는 아래와 같이 리프 노드에 위의 배열의 인덱스가 차례대로 들어갑니다.
(인덱스는 1부터 시작한다고 가정.)
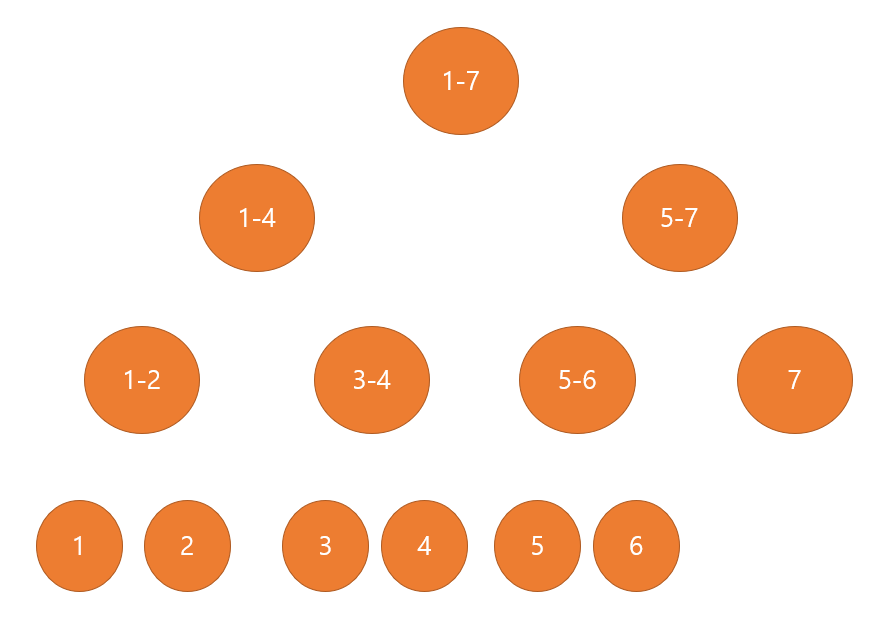
'a-b'로 표시한 부분은 a부터 b까지의 구간을 의미합니다.
리프 노드를 모두 채웠다면, 이제 구간 별로 리프 노드 중 최소 높이를 찾고, 그 높이의 실제 인덱스를 노드에 채워주시면 됩니다.
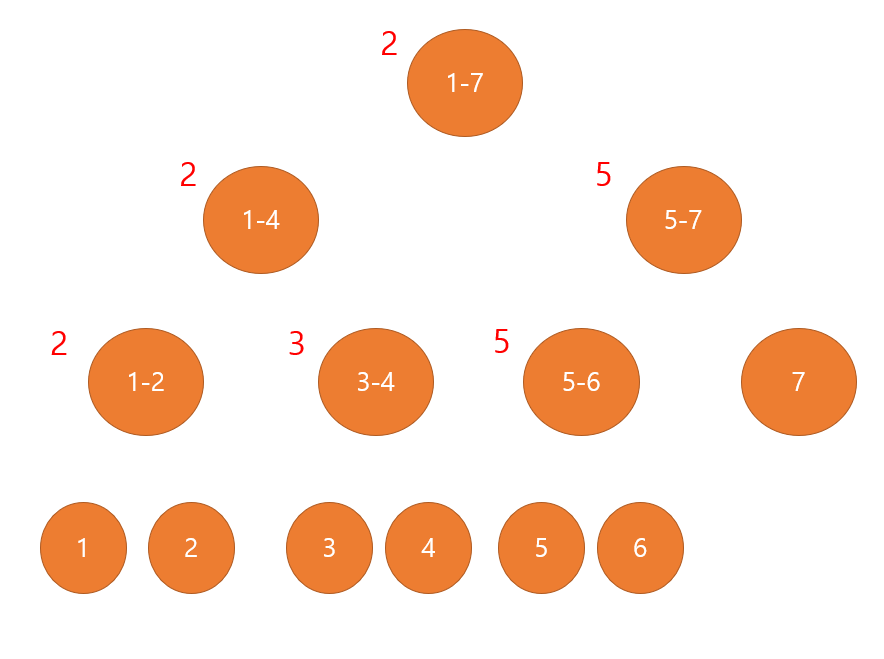
arr = { 2, 1, 4, 5, 1, 3, 3 }
(인덱스는 1부터 시작한다고 가정.)
arr[1] = 2이고, arr[2] = 1 이므로 arr[2]의 높이가 더 낮습니다. 따라서, '1-2' 구간에는 2가 들어갑니다.
arr[3] = 4이고, arr[4] = 5 이므로 arr[3]의 높이가 더 낮습니다. 따라서, '3-4' 구간에는 3이 들어갑니다.
세그먼트 트리에는 인덱스만 들어간다는 점을 유의하시면서 나머지 구간 노드를 채워주시면 됩니다.
위의 과정이 1, 2번 과정이며, init 메소드에 해당합니다.
이제, 3번 과정을 수행해야합니다.
먼저, 3번 과정을 통해서 위의 예시의 답을 도출해 내는 과정을 보여드리겠습니다.
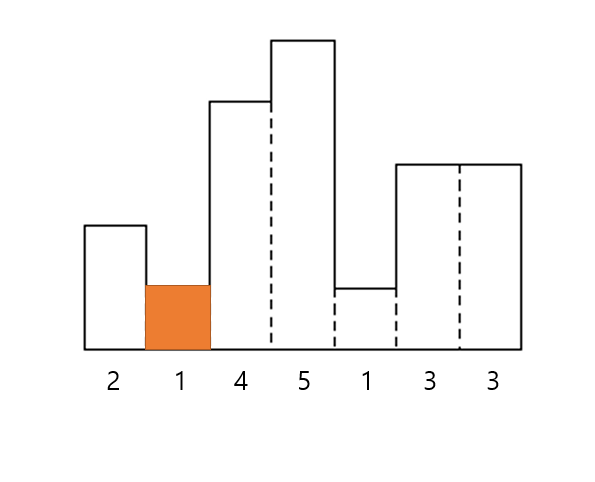
'1-7' 구간에서 가장 높이가 작은 높이는 1이며, 인덱스로는 2에 해당합니다. (5도 있지만, 더 작은 값을 우선)
따라서 직사각형의 넓이는 (7 - 1 + 1) * 1 = 7이라는 것을 알 수 있습니다.
이제, 높이를 선택한 인덱스인 2를 기준으로, 왼쪽과 오른쪽의 탐색할 수 있는 막대가 있는지 살펴봅시다.
왼쪽에는 인덱스 1이, 오른쪽에는 인덱스 3이, '1-7' 구간 내에 존재합니다.
이제, '1-1' 구간에서 직사각형의 넓이를 구해봅시다.
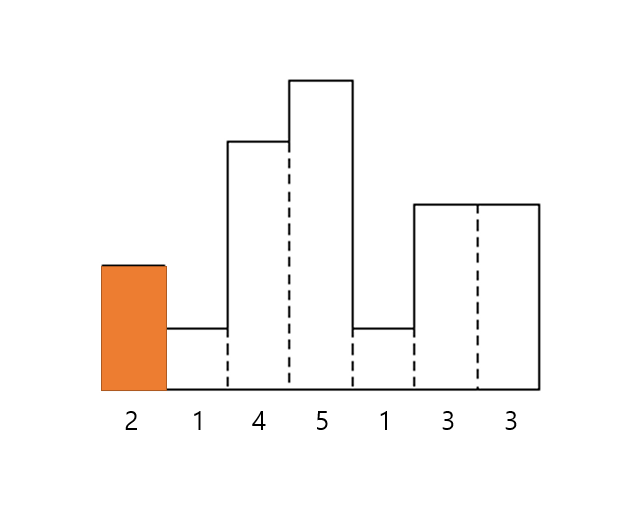
'1-1' 구간에서 높이는 2이며, 인덱스로는 1이 채택되었습니다.
따라서, 직사각형의 넓이는 (1 - 1 + 1) * 2 = 2가 됩니다.
이제, 높이를 선택한 인덱스인 1을 기준으로, 왼쪽과 오른쪽의 탐색할 수 있는 막대가 있는지 살펴봅시다.
하지만, '1-1'구간은 단순한 막대 하나이기때문에 더 이상 탐색이 불가합니다.
다시, 처음 과정에서 선택한 인덱스인 2로 돌아옵시다.
2의 오른쪽 막대인 3을 선택하여, '3-7' 구간 중 높이가 가장 작은 인덱스를 찾아서 직사각형의 넓이를 구합니다.
위와 같은 과정을 반복하면서 직사각형의 넓이가 최대가 되도록 초기화해 주면 됩니다.
이를 표현한 것이 아래 getMax 메소드입니다.
위의 코드를 보면, query라는 메소드가 보입니다.
이것은 특정 구간 내의 최소의 높이를 찾는 메소드입니다.
크게 어려운 코드는 아니니, 아래 전체 소스코드를 보면서 이해하시길 바랍니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 7578번 : 공장 (JAVA) (0) | 2020.08.20 |
|---|---|
| [BOJ] 백준 1275번 : 커피숍2 (JAVA) (0) | 2020.08.17 |
| [BOJ] 백준 2217번 : 로프 (JAVA) (0) | 2020.08.16 |
| [BOJ] 백준 10868번 : 최솟값 (JAVA) (0) | 2020.08.15 |
| [BOJ] 백준 2357번 : 최솟값과 최댓값 (JAVA) (0) | 2020.08.14 |



댓글