[BOJ] 백준 10775번 : 공항 (JAVA)
문제
오늘은 신승원의 생일이다.
박승원은 생일을 맞아 신승원에게 인천국제공항을 선물로 줬다.
공항에는 G개의 게이트가 있으며 각각은 1에서 G까지의 번호를 가지고 있다.
공항에는 P개의 비행기가 순서대로 도착할 예정이며, 당신은 i번째 비행기를 1번부터 gi (1 ≤ gi ≤ G) 번째 게이트중 하나에 영구적으로 도킹하려 한다. 비행기가 도킹된 게이트에는 다른 비행기가 도착할 수 없다.
이러한 사고가 일어나면 공항이 폐쇄되고, 이후 어떤 비행기도 도착할 수 없다.
신승원은 가장 많은 비행기를 공항에 도킹시켜서 박승원을 행복하게 하고 싶어한다. 승원이는 비행기를 최대 몇 대 도킹시킬 수 있는가?
입력
첫 번째 줄에는 게이트의 수 G (1 ≤ G ≤ 105)가 주어진다.
두 번째 줄에는 비행기의 수 P (1 ≤ P ≤ 105)가 주어진다.
이후 P개의 줄에 gi (1 ≤ gi ≤ G) 가 주어진다.
출력
승원이가 도킹시킬 수 있는 최대의 비행기 수를 출력한다.
풀이
그리디 알고리즘과 유니온 파인드 자료구조를 이용하여 풀 수 있는 문제였습니다.
우리가 눈 여겨 봐야할 점은 어떻게 비행기를 도킹시키는 것이 최선인지 판단하는 것이었습니다.
바로, g번 비행기는 g번 게이트에 차례대로 도킹을 하는 것이죠.
만약, g번 게이트가 이미 도킹이 되어있는 상태면 g-1번 게이트가 가능한지 차선책으로 확인합니다.
g-1번 게이트도 안된다면, g-2, g-3, ... , 0번 게이트까지 확인하는데, 차선책이 0번 게이트를 가리키고 있을 경우,
도킹이 불가능하다고 결론지을 수 있습니다.
이 과정에서 유니온 파인드를 사용합니다.
만약 도킹한 게이트가 g번 게이트라면, 차선책이 g-1번 게이트이므로, union(g, g-1)를 취하는 것입니다.
문제의 예시를 이용하여 다시 설명해 보겠습니다.
예제
게이트 수 : 4
비행기의 수 : 6
비행기가 도착하는 순서 : 2 - 2 - 3 - 3 - 4 - 4

사각형 4개는 게이트를 의미합니다.
먼저, 2번 비행기는 2번 게이트의 도킹하고, (2 - 1)번 째 게이트를 차선책으로 삼아서 다음에 2번 게이트에 접근하려는 비행기는 2번 대신 1번 게이트로 가게 합니다.
즉, 원은 비어있는 게이트인 차선책을 의미합니다.
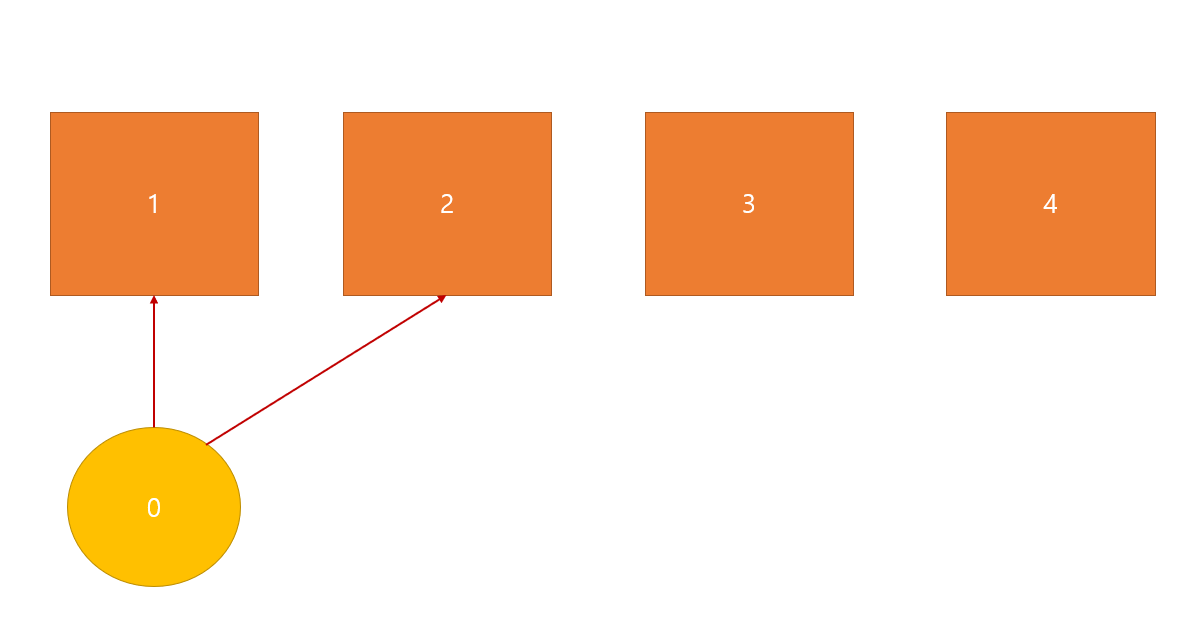
2번째로 또 2번 비행기가 들어왔습니다.
2번 게이트는 도킹되어있는 상태이므로 1번 게이트를 도킹하게한 후, 차선책으로 0번 게이트를 지정합니다.
이 때, 1, 2번 게이트 모두 차선책이 0번 게이트로 바뀐다는 사실에 유의해야합니다.

3번째로, 3번 비행기가 들어옵니다. 3번 게이트는 비어있는 상태이므로 도킹하고 차선책으로 2번 게이트를 선택하려고하지만, 2번게이트의 차선책은 0번 게이트입니다. 따라서 3번 게이트의 차선책은 0번 게이트입니다.
4번째로, 3번 비행기가 들어오지만, 차선책이 0번 게이트이므로 도킹하는 것이 불가능합니다.
따라서 도킹할 수 있는 최대 비행기의 수는 3 입니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 1647번 : 도시 분할 계획 (JAVA) (0) | 2020.08.09 |
|---|---|
| [BOJ] 백준 1922번 : 네트워크 연결 (JAVA) (0) | 2020.08.09 |
| [BOJ] 백준 2162번 : 선분 그룹 (JAVA) (0) | 2020.08.07 |
| [BOJ] 백준 4195번 : 친구 네트워크 (JAVA) (1) | 2020.08.06 |
| [BOJ] 백준 10216번 : Count Circle Groups (JAVA) (0) | 2020.08.05 |



댓글