[BOJ] 백준 2162번 : 선분 그룹 (JAVA)

문제

N개의 선분들이 2차원 평면상에 주어져 있다. 선분은 양 끝점의 x, y 좌표로 표현이 된다.

 

두 선분이 서로 만나는 경우에, 두 선분은 같은 그룹에 속한다고 정의하며, 그룹의 크기는 그 그룹에 속한 선분의 개수로 정의한다. 두 선분이 만난다는 것은 선분의 끝점을 스치듯이 만나는 경우도 포함하는 것으로 한다.

 

N개의 선분들이 주어졌을 때, 이 선분들은 총 몇 개의 그룹으로 되어 있을까? 또, 가장 크기가 큰 그룹에 속한 선분의 개수는 몇 개일까? 이 두 가지를 구하는 프로그램을 작성해 보자.

 

 

입력

첫째 줄에 N(1≤N≤3,000)이 주어진다. 둘째 줄부터 N+1번째 줄에는 양 끝점의 좌표가 x1, y1, x2, y2의 순서로 주어진다. 각 좌표의 절댓값은 5,000을 넘지 않으며, 입력되는 좌표 사이에는 빈칸이 하나 이상 있다.

 

 

출력

첫째 줄에 그룹의 수를, 둘째 줄에 가장 크기가 큰 그룹에 속한 선분의 개수를 출력한다.

 

 

풀이

기하학적 사고와 유니온 파인드를 이용하여 풀 수 있는 문제였습니다.

생각보다 예외가 많고, 우리가 중학교때 배운 일차함수 지식을 많이 떠올려서 코드에 적용하는 것이 관건이었습니다.

 

우선, 제가 푼 전반적인 로직을 소개하겠습니다.

 

 

1. p1으로 이루어진 직선과 p2로 이루어진 직선의 교점을 구한다.

(p1과 p2는 문제에서 입력받은 각각의 x와 y좌표를 의미합니다.)

 

1-1. 두 직선이 평행하거나 일치하는 경우에 대해서 p1과 p2 선분이 만나는지 확인한다.

 

1-2. 1번에서 구한 교점이 p1과 p2 선분 범위 내의 존재하는지 확인한다.

 

2. 1-1, 1-2 과정에서 선분이 만난다면 합집합 연산을 한다.

 

3. 루트 노드 배열 안의 서로 다른 요소의 개수를 세고, 같은 요소 개수 중에서 가장 큰 요소의 개수를 센다.

(서로 다른 요소의 개수는 그룹의 수고, 같은 요소 개수중에 가장 큰 요소의 개수는 그룹 내의 최대 선분의 개수이다.)

 

 

과정 자체는 심플해보입니다만, 특히 1-1번에서 예외 케이스가 많았습니다.

우선, 두 직선이 평행하거나 일치하지 않는 1-2번 경우부터 살펴보겠습니다.

 

먼저, 4개의 점이 주어졌을 때 교점을 어떻게 구할 수 있을까요?

바로, 다음과 같이 구할 수 있습니다.

 

 

 

 

출처는 이 곳에서 확인하실 수 있으며, 위 공식의 전개 과정은 우리가 배웠던 중학교 개념을 생각하시면 됩니다.

직선 A가 (x1, y1), (x2, y2)를 지나고, 직선 B는 (x3, y3), (x4, y4)를 지날 때,

A의 직선의 식은 y = m1(x - x1) + y1이고, B의 직선의 식은 y = m2(x - x3) + y3인데, B의 직선을 A의 직선에 대입하여 정리하면 위의 식이 나옵니다. 여기서 m은 기울기로, (y2 - y1) / (x2 - x1) 으로 구하시면 됩니다.

 

위의 식을 대입하면 A와 B의 직선을 구할 수 있습니다.

다만, 우리는 선분이 만나는지 파악해야하기때문에 위에서 구한 교점이 실제로 선분이 만나는 지점인지 확인해야합니다.

 

즉, 직선으로 구한 교점이 두 선분의 범위 내에 있어야합니다. 

조건식으로 쓰면,

 

x1 <= 교점X <= x2 && x3 <= 교점X <= x4 && y1 <= 교점Y <= y2 && y3 <= 교점Y <= y4

 

를 만족하면 됩니다.

 

문제는 두 직선이 평행하거나 일치하는 경우입니다.

 

먼저, 두 직선이 평행하는지 일치하는지부터 고려해야합니다.

만약, y = m1x + n1와 y = m2x + n2라는 직선이 주어졌다고 가정합시다.

그렇다면, 아래와 같이 평행과 일치를 구분할 수 있을 것입니다.

 

 

평행) m1 == m2 && n1 != n2

일치) m1 == m2 && n1 == n2

 

 

여기서, n을 식으로 표현을 어떻게 할 수 있을까요?

만약, (x1, y1), (x2, y2)라는 점이 주어졌을 때, 직선의 식은 y = m(x - x1) + y1일 것입니다.

전개를 하면, y = mx - mx1 + y1 이므로 n = -mx + y임을 알 수 있습니다.

 

따라서, 두 직선이 평행하거나 일치할 때, n1과 n2가 다르면 평행하므로 두 선분은 만나지 않는다고 판단하시면 됩니다.

하지만, 여기서 주의해야할 점이 있습니다.

 

바로, 직선의 식의 형태가 x = a일 때죠.

이것은 기울기의 분모가 0으로, 값이 무한대가 되어 버립니다.

 

따라서, x = a인 형태일 때, 따로 예외 처리를 해 주어야 합니다.

여기서도 마찬가지로 평행일 때와 일치할 때를 구분해 주어야 하는데, 두 직선의 x좌표가 서로 다르면 평행이고, 같으면 일치합니다. 평행일 때는 두 선분이 만나지 않는다고 판단하시면 됩니다.

 

일치하는 경우는 두 선분이 만나는지 어떻게 판단할까요?

여기서는 두 선분이 만나는 경우를 생각하기보다는 만나지 않는 경우를 떠올리는 것이 좋습니다.

그리고 x = a 형태일 때 두 선분이 만나지 않는 경우 단순합니다.

 

 

 

 

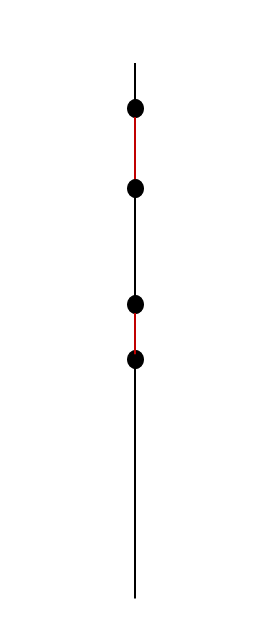
위와 같이 점 4개가 겹치지 않고 독립된 공간에 있으면 됩니다.

조건식으로 쓰면,

 

y1 > y3 && y1 > y4 && y2 > y1 && .y2 > y4 

||

y3 > y1 && y3 > y2 && y4 > y1 && y4 > y2

 

를 만족해야합니다.

 

마지막으로, x = a가 아니면서 일치하는 경우를 보겠습니다.

이 경우에는 x = a인 형태와 다르지 않습니다. 다만, x 조건만 추가해 주면 되는 것이죠.

 

위의 예외를 잘 걸러가면서 선분이 겹치는 부분은 합집합 연산을 하면 됩니다.

예를 들어, A 선분, B 선분, C 선분, D 선분이 있다고 가정합시다.

그리고 parent[i] = i로 초기화 합니다.

 

그래프 교점을 이용하다보니, A와 B 선분이 겹치고 C와 D 선분이 겹친다는 사실을 알았다고 합시다.

그렇다면, parent[0] = parent[1] = 0, parent[2] = parent[3] = 2가 될 것입니다.

 

이제, 그룹의 수와 가장 크기가 큰 그룹의 선분의 수를 구해봅시다.

저는 cnt라는 1차원 배열을 정의했습니다.

이 곳에 그룹 내의 선분의 수를 저장할 것입니다.

 

저장 방식은 간단합니다. cnt[find(i)]++ 를 취하는 것이죠.

즉, 특정 노드의 루트 노드를 찾아서, 그 루트 노드의 cnt 값을 1씩 증가시키는 것입니다.

 

위의 예시에서, cnt[0] = 2, cnt[1] = 0, cnt[2] = 2, cnt[3] = 0이 됩니다.

그룹의 수는 cnt[i] != 0인 요소의 개수고, 최대 선분의 수는 cnt[i]의 값 중 가장 큰 값에 해당합니다.

 

따라서 그룹의 개수는 2개, 가장 큰 선분의 개수는 2가 됩니다.

 

 

아래는 위 과정을 정리한 소스코드입니다.

 

 

소스코드

	import java.io.BufferedReader;
	import java.io.BufferedWriter;
	import java.io.IOException;
	import java.io.InputStreamReader;
	import java.io.OutputStreamWriter;
	import java.util.StringTokenizer;
	class Point {
	double x1;
	double y1;
	double x2;
	double y2;
	Point(double x1, double y1, double x2, double y2) {
	this.x1 = x1;
	this.y1 = y1;
	this.x2 = x2;
	this.y2 = y2;
	}
	}
	public class Main {
	static final int INF = 5000;
	static int[] parent; // 유니온 파인드 루트 노드 배열
	public static void main(String[] args) throws NumberFormatException, IOException {
	BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
	StringTokenizer st;
	int N = Integer.parseInt(br.readLine());
	parent = new int[N];
	Point[] points = new Point[N];
	for (int i = 0; i < N; i++) {
	st = new StringTokenizer(br.readLine());
	parent[i] = i;
	double x1 = Double.parseDouble(st.nextToken());
	double y1 = Double.parseDouble(st.nextToken());
	double x2 = Double.parseDouble(st.nextToken());
	double y2 = Double.parseDouble(st.nextToken());
	points[i] = new Point(x1, y1, x2, y2);
	}
	for (int i = 0; i < N; i++) {
	for (int j = i + 1; j < N; j++) {
	Point p1 = points[i];
	Point p2 = points[j];
	double res = intersectionPointX(p1, p2);
	// p1으로 이루어진 직선과 p2로 이루어진 직선이 평행 또는 일치할 경우
	if (res == INF + 1) {
	// x = a 형태인 경우
	if (p1.x2 - p1.x1 == 0 && p2.x2 - p2.x1 == 0) {
	// 두 직선이 평행
	if (p1.x1 != p2.x1) {
	continue;
	}
	// p1 선분과 p2 선분이 만나지 않음.
	if ((p1.y1 > p2.y1 && p1.y1 > p2.y2 && p1.y2 > p2.y1 && p1.y2 > p2.y2)
	|| (p2.y1 > p1.y1 && p2.y1 > p1.y2 && p2.y2 > p1.y1 && p2.y2 > p1.y2)) {
	continue;
	}
	union(i, j);
	continue;
	}
	// x = a 형태가 아닌 경우
	double m1 = (p1.y2 - p1.y1) / (p1.x2 - p1.x1);
	double m2 = (p2.y2 - p2.y1) / (p2.x2 - p2.x1);
	double n1 = -m1 * p1.x1 + p1.y1;
	double n2 = -m2 * p2.x1 + p2.y1;
	// 두 직선이 평행
	if (n1 != n2) {
	continue;
	}
	// 두 직선이 일치하지만, 각각의 선분이 만나지는 않는 경우
	if ((p1.x1 > p2.x1 && p1.x1 > p2.x2 && p1.x2 > p2.x1 && p1.x2 > p2.x2)
	|| (p2.x1 > p1.x2 && p2.x1 > p1.x2 && p2.x2 > p1.x1 && p2.x2 > p1.x2)) {
	continue;
	}
	// y = a인 형태를 고려해야 함.
	if ((p1.y1 > p2.y1 && p1.y1 > p2.y2 && p1.y2 > p2.y1 && p1.y2 > p2.y2)
	|| (p2.y1 > p1.y1 && p2.y1 > p1.y2 && p2.y2 > p1.y1 && p2.y2 > p1.y2)) {
	continue;
	}
	union(i, j);
	} else {
	// 교점이 p1 선분과 p2 선분 내의 존재해야 함.
	if (res >= Math.min(p1.x1, p1.x2) && res <= Math.max(p1.x1, p1.x2) && res >= Math.min(p2.x1, p2.x2)
	&& res <= Math.max(p2.x1, p2.x2)) {
	res = intersectionPointY(p1, p2);
	if (res <= INF && res >= -INF) {
	if (res >= Math.min(p1.y1, p1.y2) && res <= Math.max(p1.y1, p1.y2)
	&& res >= Math.min(p2.y1, p2.y2) && res <= Math.max(p2.y1, p2.y2)) {
	union(i, j);
	}
	}
	}
	}
	}
	}
	// parent의 0 ~ N까지 본인의 루트 노드에 해당하는
	// 값이 몇 개인지 계산함.
	int[] cnt = new int[N];
	for (int i = 0; i < N; i++) {
	cnt[find(i)]++;
	}
	int groupCnt = 0;
	int lineCnt = 0;
	for (int i = 0; i < N; i++) {
	// cnt가 0이 아니면 다른 노트에 대하여 합집합 연산을
	// 최소 1번이상 했다는 의미임.
	if (cnt[i] > 0) {
	groupCnt++;
	}
	lineCnt = Math.max(lineCnt, cnt[i]);
	}
	bw.write(groupCnt + "\n" + lineCnt + "\n");
	bw.flush();
	bw.close();
	br.close();
	}
	public static int find(int x) {
	if (x == parent[x]) {
	return x;
	}
	return parent[x] = find(parent[x]);
	}
	// 합집합 연산
	public static void union(int x, int y) {
	x = find(x);
	y = find(y);
	if (x != y) {
	if (x < y) {
	parent[y] = x;
	} else {
	parent[x] = y;
	}
	}
	}
	// 교점의 X좌표
	public static double intersectionPointX(Point p1, Point p2) {
	// p1로 이루어지는 직선과 p2로 이루어지는 직선이 평행 또는 일치할 경우
	// 교점 식의 분모에 해당하는 부분이 0이라는 의미
	if ((p1.x1 - p1.x2) * (p2.y1 - p2.y2) - (p1.y1 - p1.y2) * (p2.x1 - p2.x2) == 0) {
	return INF + 1;
	}
	double denominator = ((p1.x1 * p1.y2 - p1.y1 * p1.x2) * (p2.x1 - p2.x2))
	- ((p1.x1 - p1.x2) * (p2.x1 * p2.y2 - p2.y1 * p2.x2));
	double numerator = ((p1.x1 - p1.x2) * (p2.y1 - p2.y2)) - ((p1.y1 - p1.y2) * (p2.x1 - p2.x2));
	return denominator / numerator;
	}
	// 교점의 Y좌표
	public static double intersectionPointY(Point p1, Point p2) {
	// p1로 이루어지는 직선과 p2로 이루어지는 직선이 평행 또는 일치할 경우
	// 교점 식의 분모에 해당하는 부분이 0이라는 의미
	if ((p1.x1 - p1.x2) * (p2.y1 - p2.y2) - (p1.y1 - p1.y2) * (p2.x1 - p2.x2) == 0) {
	return INF + 1;
	}
	double denominator = ((p1.x1 * p1.y2 - p1.y1 * p1.x2) * (p2.y1 - p2.y2)
	- (p1.y1 - p1.y2) * (p2.x1 * p2.y2 - p2.y1 * p2.x2));
	double numerator = ((p1.x1 - p1.x2) * (p2.y1 - p2.y2) - (p1.y1 - p1.y2) * (p2.x1 - p2.x2));
	return denominator / numerator;
	}
	}

view raw 2162.java hosted with ❤ by GitHub

 

지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.