[BOJ] 백준 1865번 : 웜홀 (JAVA)
문제
때는 2020년, 백준이는 월드나라의 한 국민이다. 월드나라에는 N개의 지점이 있고 N개의 지점 사이에는 M개의 도로와 W개의 웜홀이 있다. (단 도로는 방향이 없으며 웜홀은 방향이 있다.) 웜홀은 시작 위치에서 도착 위치로 가는 하나의 경로인데, 특이하게도 도착을 하게 되면 시작을 하였을 때보다 시간이 뒤로 가게 된다. 웜홀 내에서는 시계가 거꾸로 간다고 생각하여도 좋다.
시간 여행을 매우 좋아하는 백준이는 한 가지 궁금증에 빠졌다. 한 지점에서 출발을 하여서 시간여행을 하기 시작하여 다시 출발을 하였던 위치로 돌아왔을 때, 출발을 하였을 때보다 시간이 되돌아가 있는 경우가 있는지 없는지 궁금해졌다. 여러분은 백준이를 도와 이런 일이 가능한지 불가능한지 구하는 프로그램을 작성하여라.
입력
첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다. 그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500), 도로의 개수 M(1 ≤ M ≤ 2500), 웜홀의 개수 W(1 ≤ W ≤ 200)이 주어진다.
그리고 두 번째 줄부터 M+1개의 줄에 도로의 정보가 주어지는데 각 도로의 정보는 S, E, T 세 정수로 주어진다. S와 E는 연결된 지점의 번호, T는 이 도로를 통해 이동하는데 걸리는 시간을 의미한다. 그리고 M+2~M+W+1번째 줄까지 웜홀의 정보가 S, E, T 세 정수로 주어지는데 S는 시작 지점, E는 도착 지점, T는 줄어드는 시간을 의미한다. T는 10,000보다 작거나 같은 자연수 또는 0이다.
두 지점을 연결하는 도로가 한 개보다 많을 수도 있다. 지점의 번호는 1부터 N까지 자연수로 중복 없이 매겨져 있다.
출력
TC개의 줄에 걸쳐서 만약에 시간이 줄어들면서 출발 위치로 돌아오는 것이 가능하면 YES, 불가능하면 NO를 출력한다.
풀이
벨만포드 알고리즘의 기초 문제였습니다.
혹시 벨만포드 알고리즘이 처음이신 분은 아래 포스팅을 정독하고 오시길 바랍니다.
벨만-포드 알고리즘 · ratsgo's blog
이번 글에서는 최단 경로(Shortest Path)를 찾는 대표적인 기법 가운데 하나인 벨만-포드 알고리즘(Bellman-Ford’s algorithm)을 살펴보도록 하겠습니다. 이 글은 고려대 김선욱 교수님과 역시 같은 대학��
ratsgo.github.io
간단히 말하면, (정점의 개수 - 1)번 동안 그래프 내의 모든 간선을 보면서 최단거리 배열(dist)를 계속 업데이트를 하는 작업입니다. 문제에서 웜홀은 줄어드는 시간은 의미하므로 음수 가중치임을 알 수 있습니다.
따라서 다익스트라 알고리즘은 사용할 수 없고, 벨만 포드 알고리즘을 이용하여 음수 사이클이 발생하는지 체크하면 됩니다.
여기서 음수 사이클은 아래 그림을 통해 알아봅시다.

A를 시작점으로 잡는다면, dist[A] = 0이고, dist[B] = INF일 것입니다.
이를 계속해서 왔다갔다하면 최단거리가 dist[A] = -2, -4, -6, .... 으로, 무한 초기화된다는 것을 알 수 있습니다.
문제에서는 시간이 되돌아가 있는 경우를 찾으라고 명시했기때문에 음의 사이클이 발생하는지 확인하여야 합니다.
기본적으로 벨만포드 알고리즘은 (정점의 개수 - 1)번까지만 최단거리 업데이트 작업을 하기 때문에 (정점의 개수)번까지도 업데이트를 실행할 경우, 음의 사이클이 발생했다는 것을 알 수 있습니다.
이 문제를 푸는 방식은 2가지가 있습니다.
1. 모든 정점을 출발점으로 조사해서 음의 사이클이 발생하는지 확인
2. 아무 정점을 출발점으로 조사해서 음의 사이클이 발생하는지 확인
풀이 - 첫 번째 방식
문제를 가장 충실히 반영한 방법입니다. 문제에서는 출발점을 명시하지 않았기때문에 모든 정점을 출발점으로 삼고, 벨만포드 알고리즘을 그대로 구현하면 됩니다.
소스코드 - 첫 번째 방식
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
|
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
class Road {
int end;
int weight;
Road(int end, int weight) {
this.end = end;
this.weight = weight;
}
}
public class Main {
static int N, M, W;
static int[] dist;
static ArrayList<ArrayList<Road>> a;
static final int INF = 987654321;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int TC = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (TC-- > 0) {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
dist = new int[N + 1];
a = new ArrayList<>();
for (int i = 0; i <= N; i++) {
a.add(new ArrayList<>());
}
for (int i = 0; i < M + W; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
if (i < M) { // 도로는 양방향 그래프
a.get(start).add(new Road(end, weight));
a.get(end).add(new Road(start, weight));
} else { // 웜홀은 단방향 그래프
a.get(start).add(new Road(end, -weight));
}
}
boolean isMinusCycle = false;
for (int i = 1; i <= N; i++) {
if (bellmanFord(i)) {
isMinusCycle = true;
sb.append("YES\n");
break;
}
}
if (!isMinusCycle) {
sb.append("NO\n");
}
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
// 벨만포드 알고리즘
public static boolean bellmanFord(int start) {
Arrays.fill(dist, INF);
dist[start] = 0; // 시작점은 0으로 초기화.
boolean update = false;
// (정점의 개수 - 1)번 동안 최단거리 초기화 작업을 반복함.
for (int i = 1; i < N; i++) {
update = false;
// 최단거리 초기화.
for (int j = 1; j <= N; j++) {
for (Road road : a.get(j)) {
if (dist[j] != INF && dist[road.end] > dist[j] + road.weight) {
dist[road.end] = dist[j] + road.weight;
update = true;
}
}
}
// 더 이상 최단거리 초기화가 일어나지 않았을 경우 반복문을 종료.
if (!update) {
break;
}
}
// (정점의 개수 - 1)번까지 계속 업데이트가 발생했을 경우
// (정점의 개수)번도 업데이트 발생하면 음수 사이클이 일어난 것을 의미함.
if (update) {
for (int i = 1; i <= N; i++) {
for (Road road : a.get(i)) {
if (dist[i] != INF && dist[road.end] > dist[i] + road.weight) {
return true;
}
}
}
}
return false;
}
}
|
cs |
풀이 - 두 번째 방식
문제에서는 출발점을 알려주지 않았는데, 우리는 하나의 정점만을 택하고 벨만포드 알고리즘을 "1번"만 수행해도 음의 사이클이 발생하는지 알 수 있습니다.
첫 번째 방식 소스코드를 유심히 살펴보면, 중간에 dist[i] != INF 조건이 있습니다.
이것은 아직 방문하지 않은 단절된 곳을 의미하며, 이 곳을 시작점으로 삼아서 다른 곳으로 이동하는 것은 불가능합니다.
가령, 아래와 같은 그래프가 있다고 가정합시다.
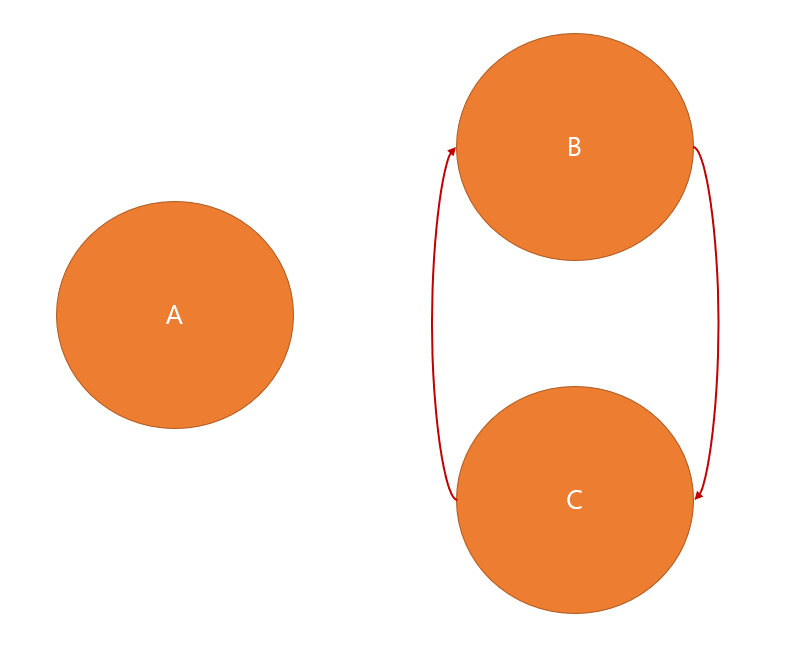
만약, 출발점이 A라고 한다면, dist[A] = 0, dist[B] = dist[C] = INF일 것입니다. 그리고 첫 번째 풀이 방식에서 사용한 INF 조건을 추가하면, A에서는 다른 곳으로 탐색할 수가 없습니다. 하지만, B와 C에서는 음의 사이클이 발생할 수도 있습니다.
이 문제를 틀린 다른 사람들의 코드를 살펴 보니, 출발점은 1로 잡아 놓고, INF 조건을 추가한 경우가 많았습니다.
참고 URL
글 읽기 - INF비교가 없어야 하는 이유가 뭘까요?
댓글을 작성하려면 로그인해야 합니다.
www.acmicpc.net
즉, INF 조건을 제거하고 dist 배열의 초기값은 -1이나 987654321과 같은 오버플로우가 발생하지 않는 적절한 값으로 초기화 한 뒤, 벨만포드 알고리즘을 수행하면 음의 사이클을 찾을 수 있습니다. dist 배열의 초기값을 적절한 값으로 초기화해도 되는 이유는, 우리가 최단거리를 구하는 것이 아니라 단순히 사이클만 찾아야하기 때문이죠.
아래는 위 과정을 정리한 소스코드입니다.
소스코드 - 두 번째 방식
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
|
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
class Road {
int end;
int weight;
Road(int end, int weight) {
this.end = end;
this.weight = weight;
}
}
public class Main {
static int N, M, W;
static int[] dist;
static ArrayList<ArrayList<Road>> a;
static final int INF = 987654321;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int TC = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (TC-- > 0) {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
dist = new int[N + 1];
a = new ArrayList<>();
for (int i = 0; i <= N; i++) {
a.add(new ArrayList<>());
}
for (int i = 0; i < M + W; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
if (i < M) { // 도로는 양방향 그래프
a.get(start).add(new Road(end, weight));
a.get(end).add(new Road(start, weight));
} else { // 웜홀은 단방향 그래프
a.get(start).add(new Road(end, -weight));
}
}
sb.append(bellmanFord() ? "YES\n" : "NO\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
// 벨만포드 알고리즘
public static boolean bellmanFord() {
Arrays.fill(dist, INF);
dist[1] = 0; // 시작점은 0으로 초기화.
boolean update = false;
// (정점의 개수 - 1)번 동안 최단거리 초기화 작업을 반복함.
for (int i = 1; i < N; i++) {
update = false;
// 최단거리 초기화.
for (int j = 1; j <= N; j++) {
for (Road road : a.get(j)) {
if (dist[road.end] > dist[j] + road.weight) {
dist[road.end] = dist[j] + road.weight;
update = true;
}
}
}
// 더 이상 최단거리 초기화가 일어나지 않았을 경우 반복문을 종료.
if (!update) {
break;
}
}
// (정점의 개수 - 1)번까지 계속 업데이트가 발생했을 경우
// (정점의 개수)번도 업데이트 발생하면 음수 사이클이 일어난 것을 의미함.
if (update) {
for (int i = 1; i <= N; i++) {
for (Road road : a.get(i)) {
if (dist[road.end] > dist[i] + road.weight) {
return true;
}
}
}
}
return false;
}
}
|
cs |
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 1219번 : 오만식의 고민 (JAVA) (0) | 2020.07.29 |
|---|---|
| [BOJ] 백준 11657번 : 타임머신 (JAVA) (0) | 2020.07.28 |
| [BOJ] 백준 14938번 : 서강그라운드 (JAVA) (0) | 2020.07.26 |
| [BOJ] 백준 2014번 : 소수의 곱 (JAVA) (1) | 2020.07.24 |
| [BOJ] 백준 2696번 : 중앙값 구하기 (JAVA) (0) | 2020.07.22 |



댓글