[데이터베이스] B-Tree 인덱스를 보편적으로 사용하는 이유
cs-study에서 스터디를 진행하고 있습니다.
Tree 자료 구조
평균 시간 복잡도
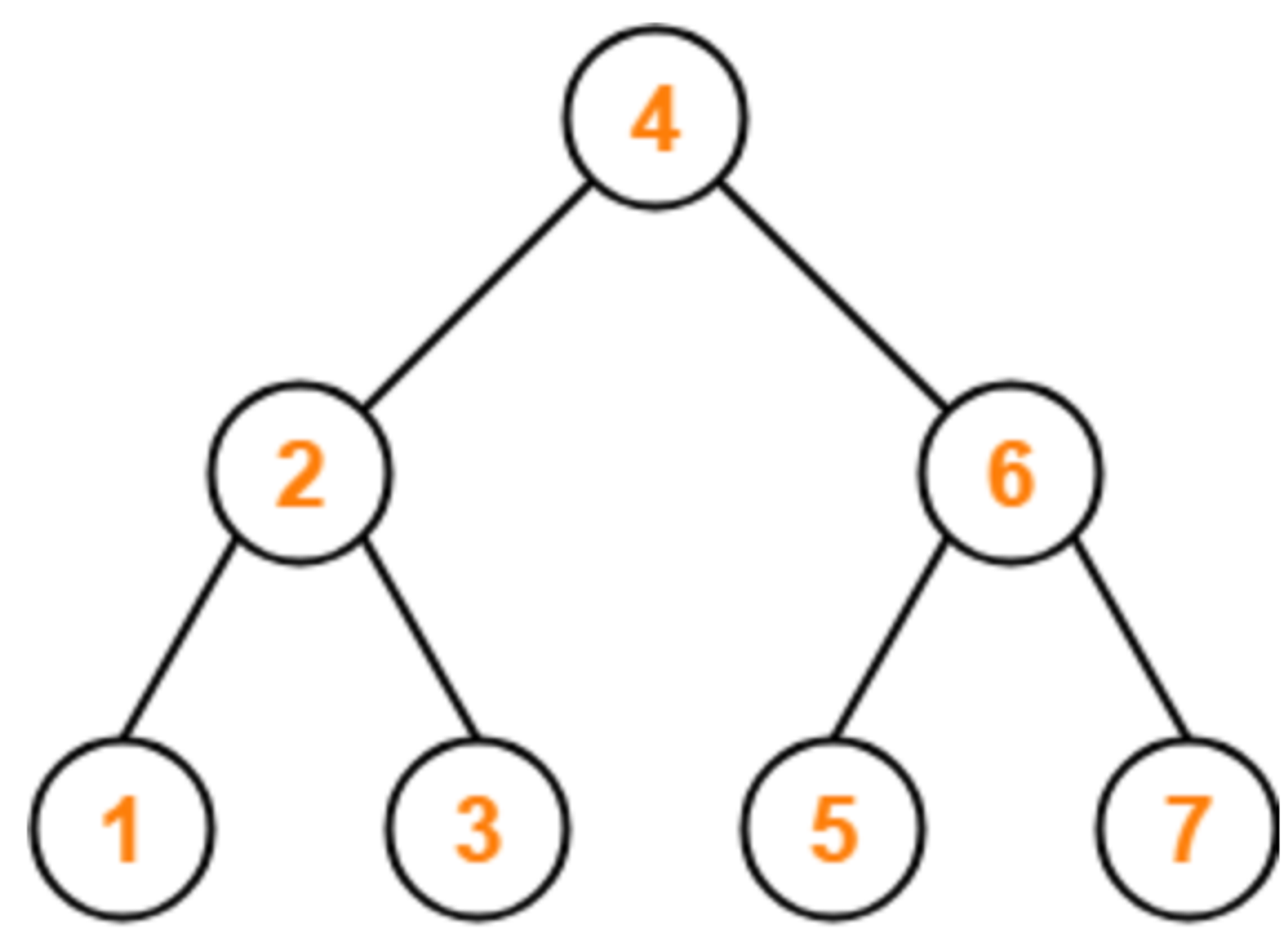
일반적인 Tree는 탐색하는 시간 복잡도가 O(logN)을 갖는다. 그러나 일반적이지 않고 특수한 경우는 어떨까?
최악 시간 복잡도
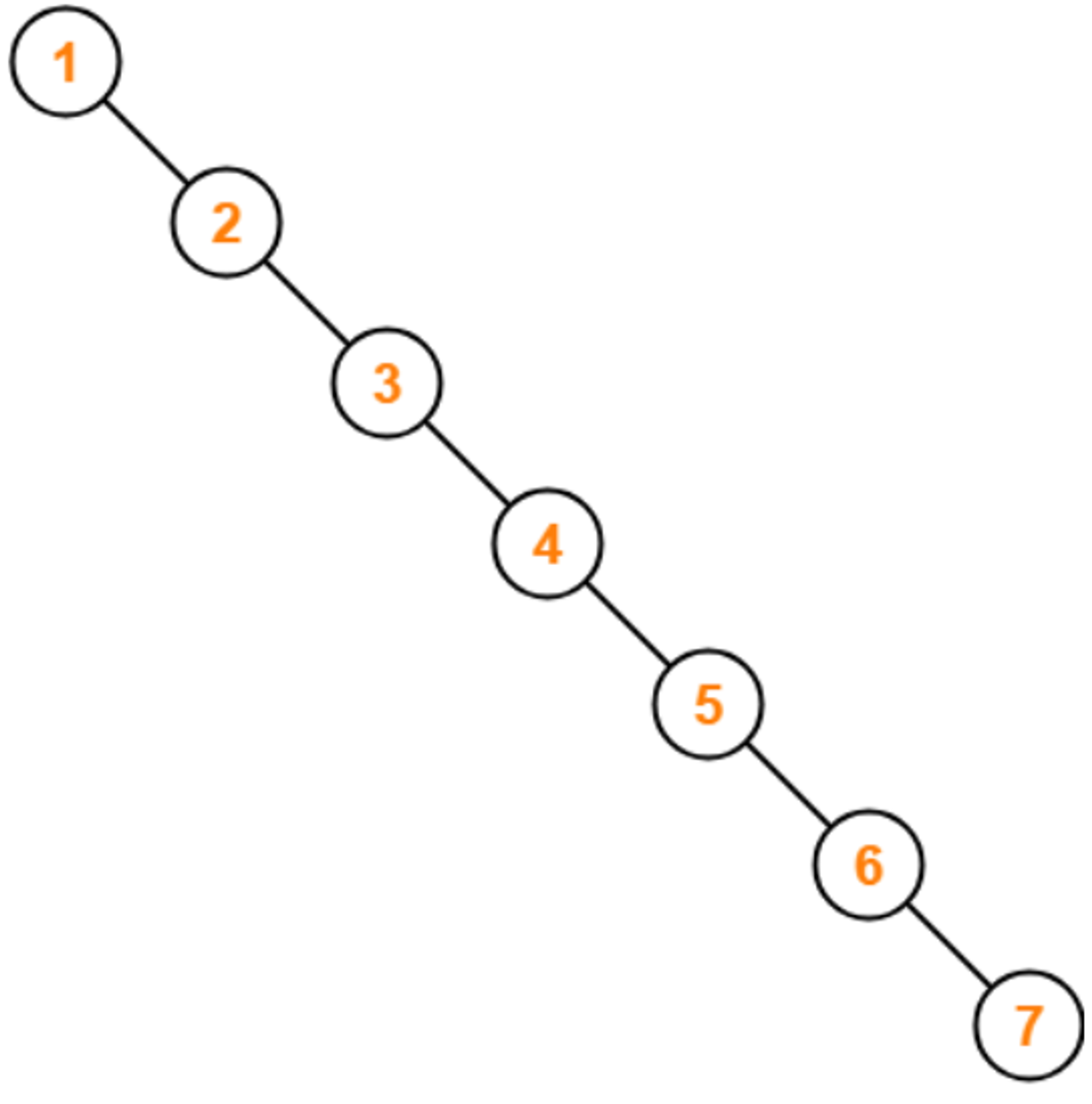
트리 노드의 요소가 한 쪽으로 쏠리게 되면, 시간 복잡도가 O(N)을 갖게 되어 List와 별반 다를 것이 없어진다. 이러한 경우를 방지하기 위하여 인덱스에서는 밸런스 트리를 선택하였다.
밸런스 트리 (Balanced Tree)
트리의 노드가 한 방향으로 쏠리지 않도록, 노드 삽입 및 삭제 시 특정 규칙에 맞게 재 정렬되어 왼쪽과 오른쪽 자식 양쪽 수의 밸런스를 유지하는 트리이다. 항상 양쪽 자식의 밸런스를 유지하므로 무조건 O(logN)의 시간 복잡도를 보장한다. 다만 재 정렬되는 작업으로 인해 노드 삽입 및 삭제 시 일반적인 트리보다 성능이 떨어진다. 그러므로 밸런스 트리는 삽입/삭제의 성능을 희생하고 탐색에 대한 성능을 높였다고 볼 수 있다.
밸런스 트리는 대표적으로 RedBlack-Tree, B-Tree가 있다.
RedBlack-Tree vs B-Tree
둘 다 밸런스 트리인데, 왜 데이터베이스는 보편적으로 인덱스의 자료 구조로 B-Tree를 선택했을까? 그것은 각각의 트리가 사용하고 있는 자료 구조의 동작 원리를 살펴 보아야 한다.
다만 자세한 동작 원리는 최하단 출처의 포스팅으로 대체하고, B-Tree가 인덱스로 선택된 이유를 바탕으로 설명하고자 한다.
RedBlack-Tree의 특징
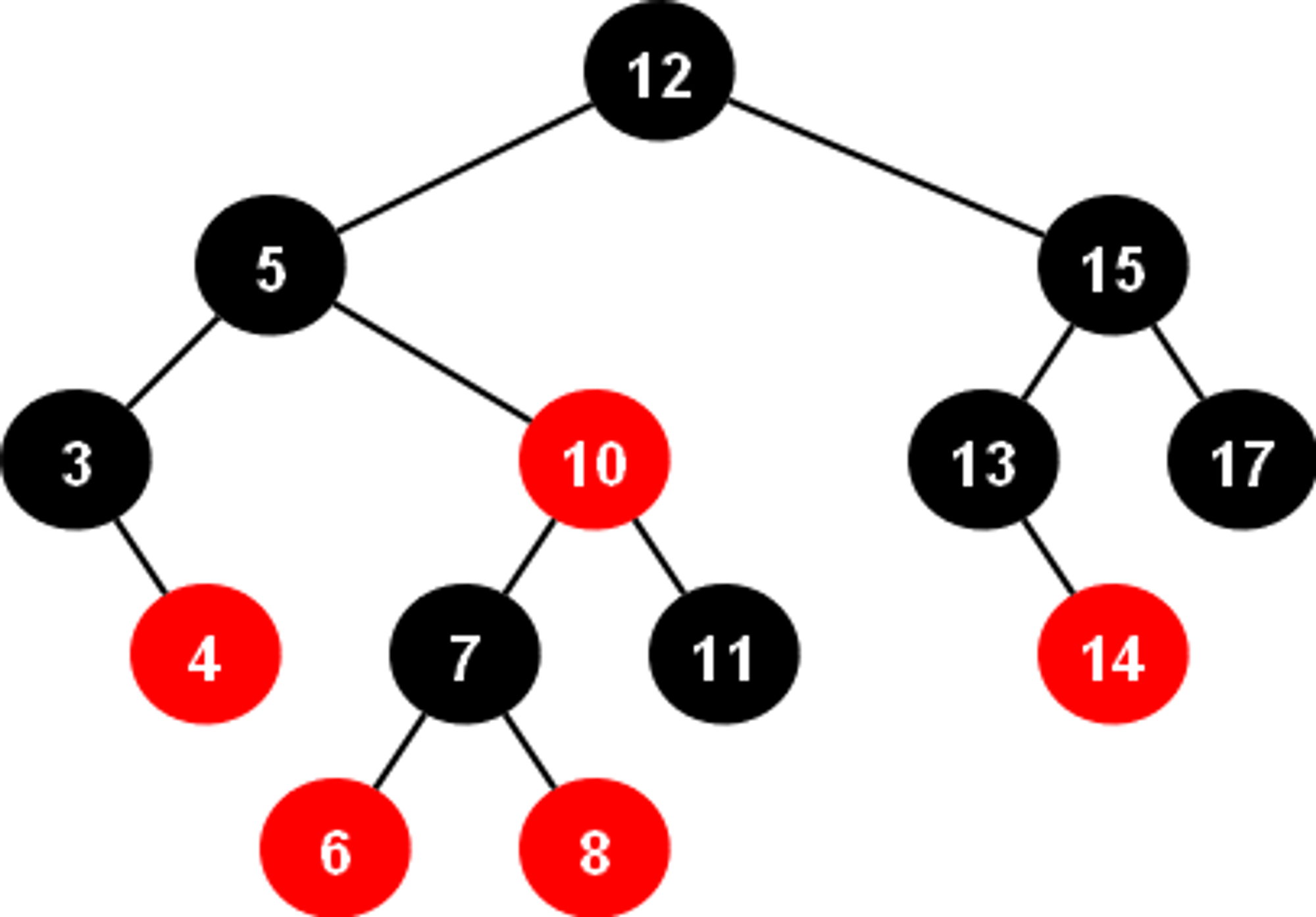
각 노드는 하나의 데이터만 가진 상태로 좌,우 자식 노드의 개수 밸런스를 맞추며, 빨간색과 검은색 노드는 재 정렬을 위해 사용되는 수단이다.
B-Tree의 특징

각 노드는 여러 데이터가 저장될 수 있으며, 각 노드 내 데이터는 항상 정렬된 상태이다. 데이터와 데이터 사이의 범위를 이용하여 자식 노드를 가지며, 자식 노드 개수는 (n+1)개이다.
두 자료 구조의 공통점과 차이점
공통점
항상 좌, 우 자식 노드 개수의 밸런스를 유지하므로 항상 시간 복잡도 O(logN)을 보장한다.
차이점
위에서 굵은 글씨 표시를 했듯이, 하나의 노드가 가지는 데이터의 개수가 다르다. RedBlack-Tree는 무조건 하나의 노드에 하나의 데이터 요소만을, B-Tree는 하나의 노드에 여러 개의 데이터를 저장한다.
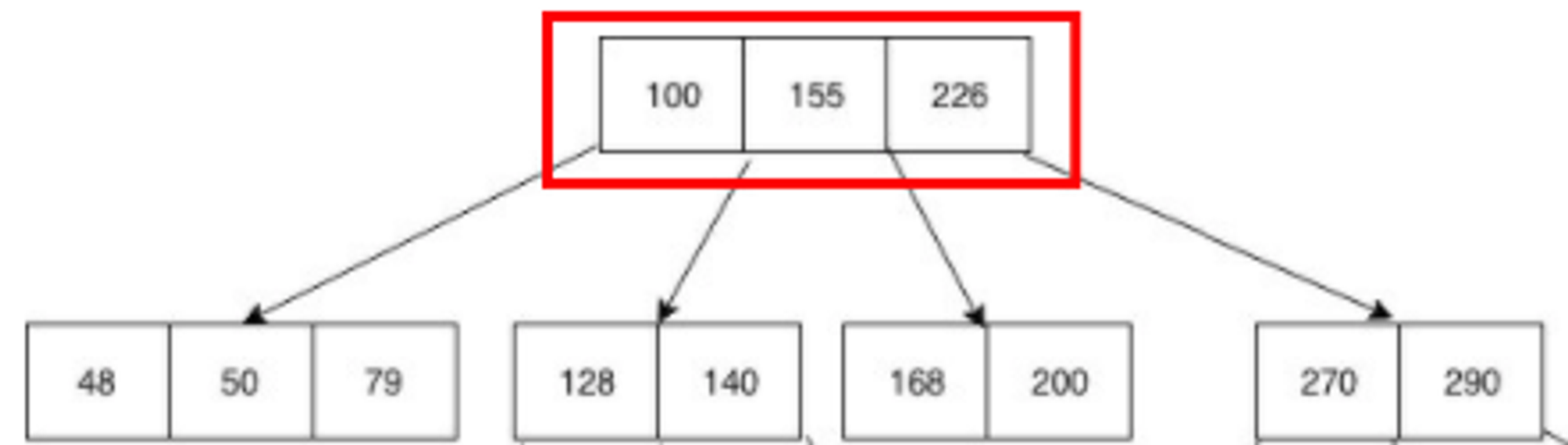
B-Tree의 각 노드는 배열로서 실제 메모리 상에 차례대로 저장이 되어 있다. 같은 노드 공간의 데이터들끼리 굳이 자식 노드처럼 참조 포인터 값으로 접근할 필요가 없다. 즉, 같은 노드 상 데이터를 탐색할 때는 포인터 접근을 하는 것이 아니라 실제 메모리 디스크에서 바로 다음 인덱스에 접근을 하는 것이다.
[탐색 방식]
- 200이라는 값이 있는지 확인하기 위해 100, 155, 226이 저장되어 있는 Root 노드에 있는 데이터를 탐색한다. 실제 메모리 디스크 상 순차적으로 저장되어 있는 데이터를 빠르게 탐색한다.
- Root 노드에 200이 없다. 200은 155와 226 사이의 값이므로 해당 범위에 존재하는 자식 노드를 가리키는 포인터가 존재하는지 확인한다. 있으면 포인터를 통해 해당 자식 노드로 접근한다. 자식 노드는 168, 200의 값을 가지고 있다.
- 실제 메모리 디스크 상 순차적으로 저장되어 있는 168, 200의 값을 빠르게 탐색한다. 찾으려 했던 200의 값을 찾아낸다.
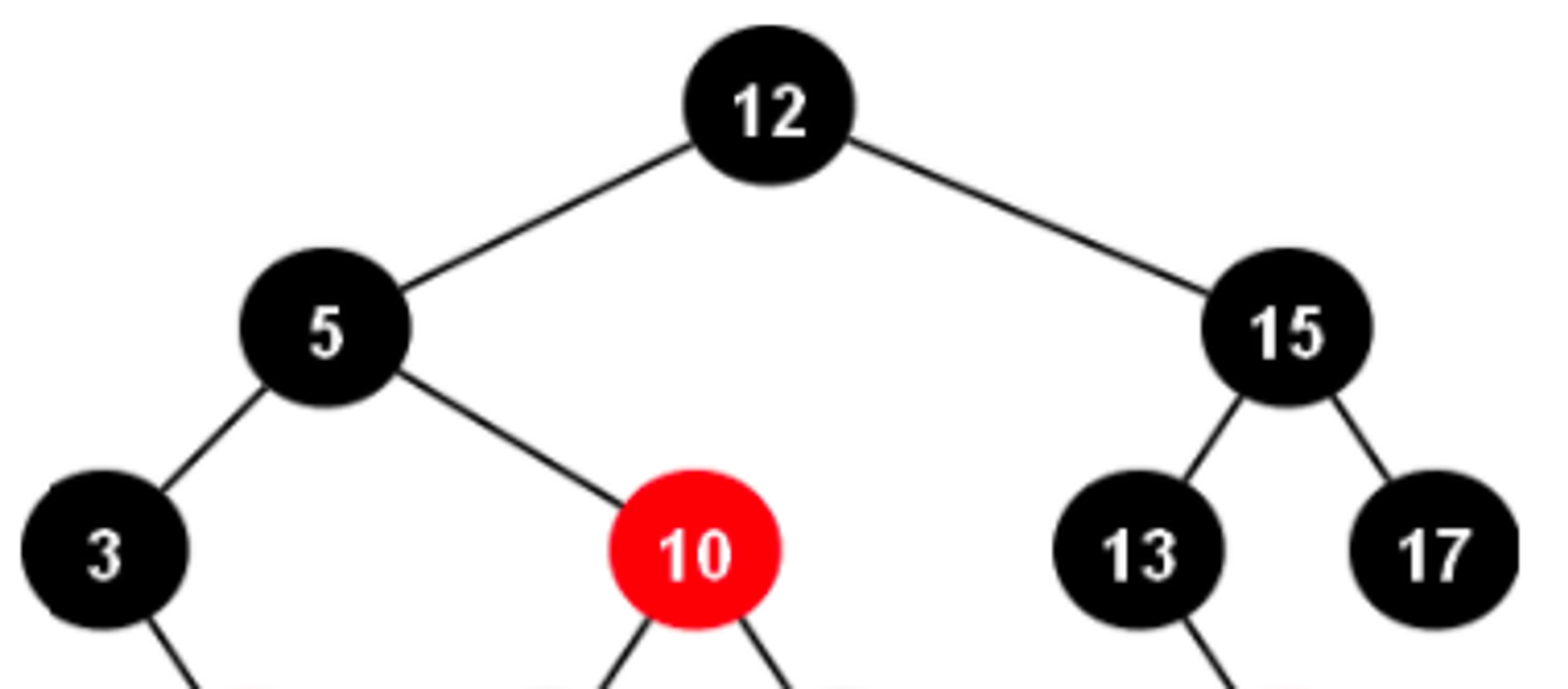
반면 RedBlack-Tree는 각 노드마다 무조건 하나의 데이터만 가지게 되므로 모든 데이터를 접근할 때 무조건 참조 포인터로 접근한다. 따라서 B-Tree의 배열 형식의 접근과 RedBlack-Tree의 참조 포인터 접근의 시간 차이를 알아야 한다.
참조 포인터로 메모리에 접근한다는 것은 실제 메모리 상 순서대로 저장이 되었든 안 되었든 접근하려는 주소를 연산을 통해 직접 알아 내어 데이터에 접근한다는 뜻이다. 주소를 알아내기 위해 CPU 내부적으로 많은 연산을 수행한다.
배열은 데이터들이 메모리 공간에 차례대로 저장이 되어 있으므로 접근할 주소를 배열의 인덱스를 사용하여 바로 알 수 있다. 그래서 메모리 주소를 알아내기 위한 추가 연산이 필요 없다. 비록 B-Tree도 자식 노드를 접근할 때는 참조 포인터로 접근을 하지만, 하나의 노드가 가지는 데이터 개수가 많아질수록 포인터 개수는 확연히 줄어 들고, 트리 내에서 다루는 데이터가 많아질수록 이러한 차이는 커진다.
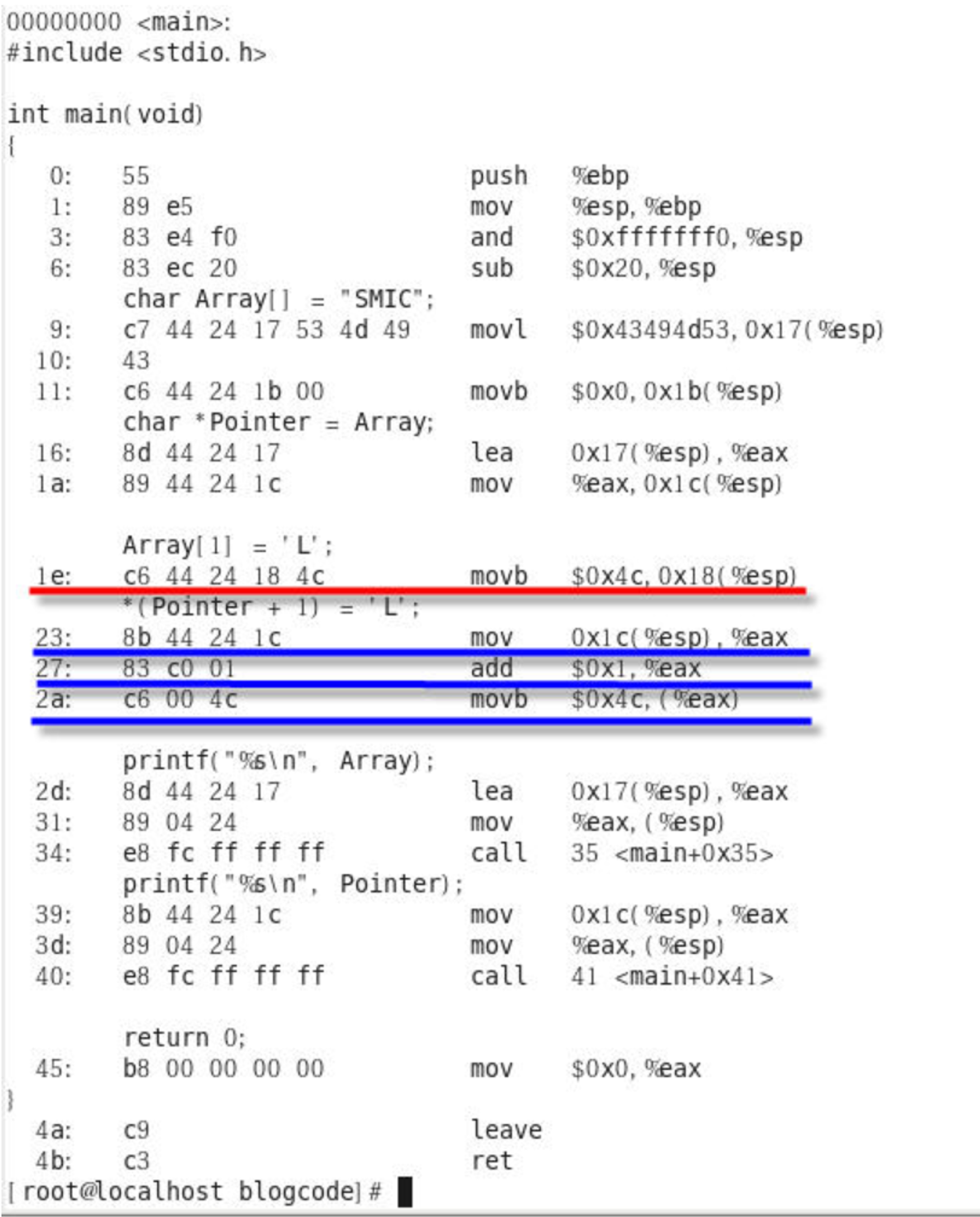
위는 인덱스와 포인터를 사용한 c언어 코드를 어셈블리어로 번역한 것이다. 빨간색 밑줄은 배열을 인덱스로 접근하였고, 파란색 밑줄은 배열은 포인터로 접근한 것을 나타낸다. 인덱스로 배열을 접근할 때는 단순하게 값을 대입하는 연산만 있지만, 포인터는 배열의 맨 처음 바이트 블럭의 주소로 이동하는 연산과 그 주소에서 xByte만큼 주소를 더하는 덧셈 연산과 마지막으로 실제 배열에 넣을 값을 대입하는 연산이 수행된다. (x는 int냐 char냐에 따라 바이트가 달리진다. 이 예제에서는 배열에 넣을 값의 자료형이 char이므로 8이 된다.)
둘 다 이론적인 시간 복잡도는 동일하지만, 포인터 접근 수의 차이로 인해 B-Tree가 탐색 시간이 더욱 빠르다.
참고로 B-Tree는 각 노드의 가질 수 있는 데이터를 3개 또는 5개 정도로 상수 시간으로 제한하고 있으므로, 각 노드 배열에서 탐색하는 시간 복잡도는 고려하지 않아도 된다.
결론
참조 포인터 접근의 수 때문에 RedBlack-Tree가 아닌, B-Tree를 인덱스의 자료 구조로 선택하였다.
배열 자료 구조
배열은 참조 포인터라는 개념이 없고, 모든 데이터가 메모리 상 차례대로 저장되어 있으므로 배열의 인덱스를 통해 O(1)의 시간 복잡도로 요소를 조회할 수 있다. 참조가 없으니 당연히 탐색 속도로는 B-Tree보다 훨씬 빠르다. 그리고 해시 테이블은 아래에서 자세히 다루겠지만, 해시 테이블과는 다르게 데이터를 정렬 상태로 유지할 수 있으므로 부등호 연산에도 문제가 없다.
하지만 배열이 B-Tree보다 빠른 것은 오직 탐색 뿐이다. 배열 내에서 데이터의 저장이나 삭제가 일어나는 순간 B-Tree보다 훨씬 성능이 떨어진다.
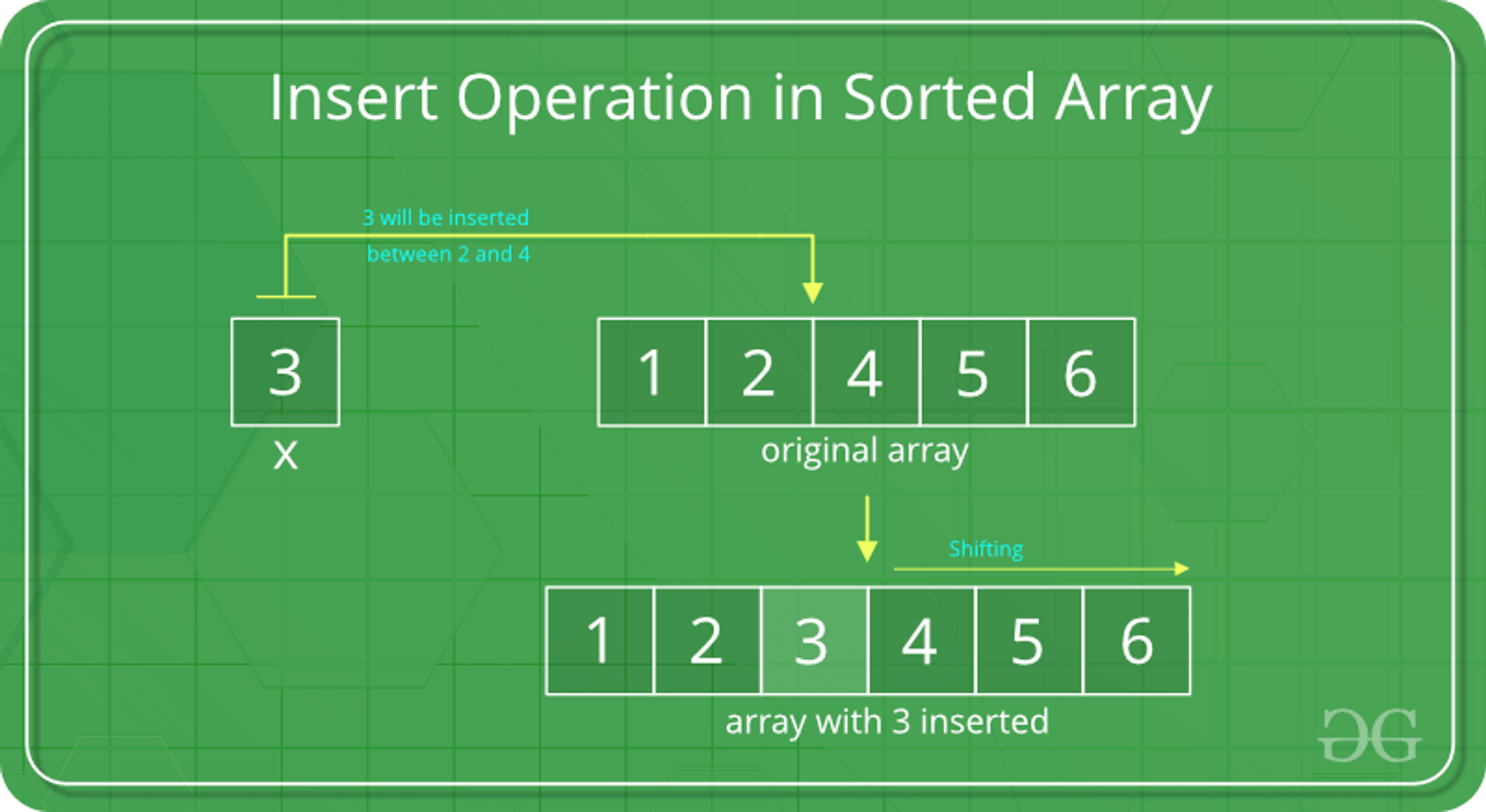
위 사진처럼 중간에 3이라는 데이터를 삽입하게 되면, 삽입될 자리를 찾은 뒤 3보다 큰 데이터는 한 칸씩 모두 뒤로 밀어야 한다. 반대로 삭제 연산이 발생하면 삭제할 자리를 찾아서 지우고, 그것보다 큰 데이터를 모두 앞으로 밀어야 한다. 그래서 시간 복잡도는 최대 O(N)을 갖게 된다.
또한, 데이터 수정이 발생할 때는 정렬을 해야 하므로 시간 복잡도 O(NlogN) 작업을 수행해야 한다.
참고로 B-Tree의 삽입과 삭제는 트리의 높이(h)에 따른 O(h)의 시간 복잡도를 가지는데, 이것은 N보다 훨씬 작은 값이다.
결론
데이터 저장, 수정, 삭제 시 배열이 B-Tree보다 월등히 느리므로 배열이 아닌, B-Tree를 인덱스의 자료 구조로 선택하였다.
해시 테이블 자료 구조
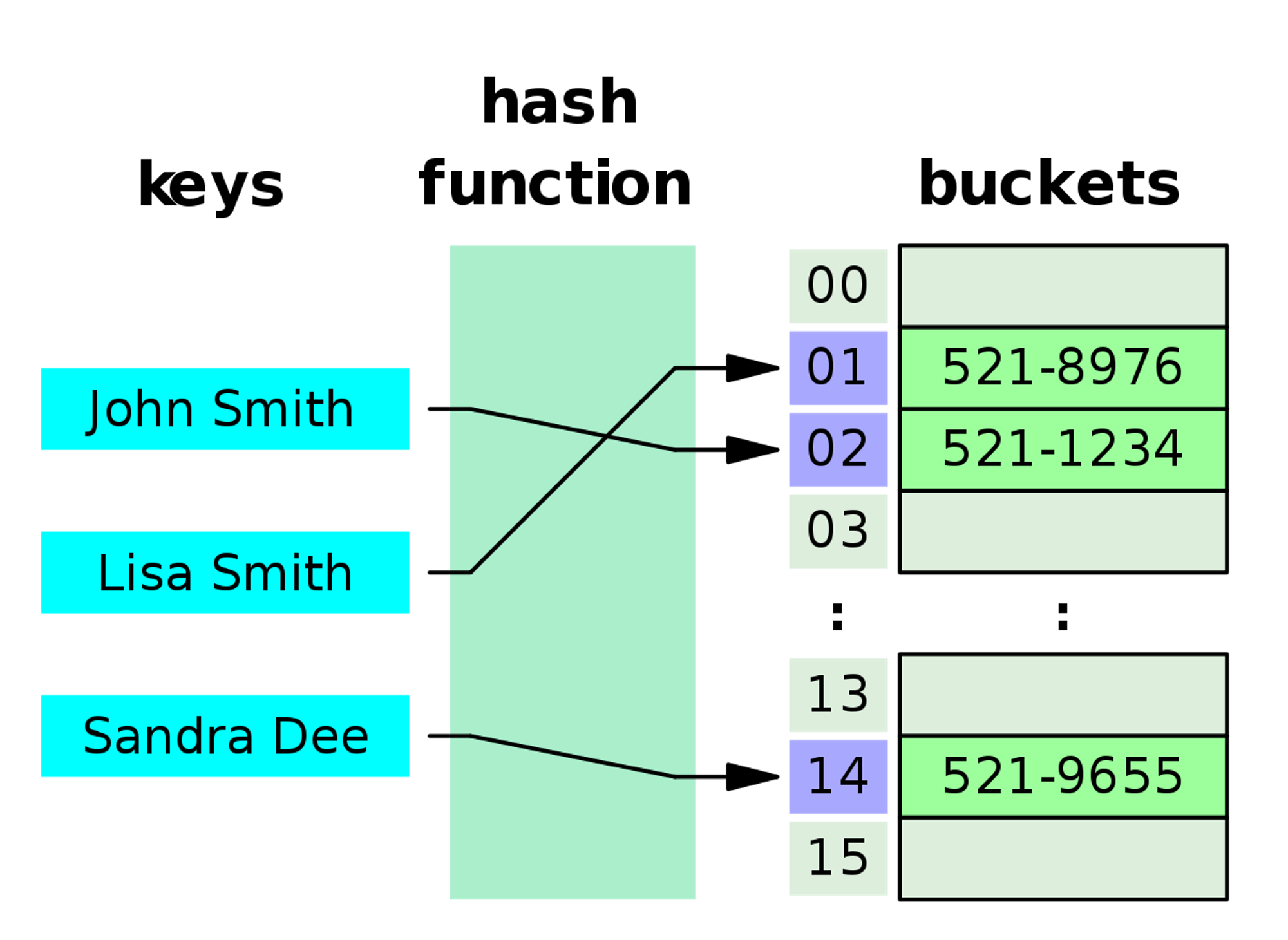
해시 테이블은 해시 함수를 통해 나온 해시 값을 이용하여 저장된 메모리 공간에 한 번에 접근하므로 O(1)이라는 시간 복잡도를 갖는다. 물론 해시 충돌 등으로 최악의 경우에는 O(N)이 될 수 있지만, 평균적으로는 O(1)이다.
그러나 이는 온전히 단 하나의 데이터를 탐색하는 시간에만 O(1)이다. 만약, 부등호 연산을 사용하게 된다면 어떻게 될까?
해시 테이블은 모든 값이 정렬되어 있지 않으므로 특정 기준보다 크거나 작은 값을 찾을 수 없다. 굳이 찾으려면 가능하겠지만 O(1)의 시간 복잡도를 보장할 수 없고 매우 비효율적이다. 그렇기에 기준 값보다 크거나 작은 요소를 탐색할 수 있어야 하는 DB 인덱스 용도로 해시 테이블은 적합하지 않은 것이다.
다만, 등호 연산에서 해시 테이블은 훌륭한 성능을 자랑하므로 특정 경우에만 해시 인덱스를 적용하여 사용할 때도 있다. 이것은 다음 포스팅에서 설명하려고 한다.
결론
부등호 연산이 불가능하므로 해시 테이블이 아닌, B-Tree를 인덱스의 자료 구조로 선택하였다.
출처
- https://helloinyong.tistory.com/296
- https://velog.io/@emplam27/자료구조-그림으로-알아보는-B-Tree
- https://zeddios.tistory.com/237
예상 면접 질문 및 답변
왜 보편적으로 레드 블랙 트리 대신 B-Tree 자료 구조를 DB 인덱스로 사용하는가?
RedBlack-Tree는 무조건 하나의 노드에 하나의 데이터 요소만을 저장하므로 어떠한 요소를 탐색하든 참조 포인터 접근이 필수적이다. 반면, B-Tree는 하나의 노드에 여러 개의 데이터를 저장하므로 각 노드의 데이터 요소를 탐색할 때 참조 포인터 접근 없이 배열의 성질을 이용하여 빠르게 탐색이 가능하다. 결론적으로 참조 포인터의 접근 수가 B-Tree가 훨씬 적으므로 B-Tree를 인덱스의 자료 구조로 사용한다.
왜 보편적으로 배열 대신 B-Tree 자료 구조를 DB 인덱스로 사용하는가?
배열은 데이터를 조회할 때만 B-Tree보다 빠르고, 나머지 데이터 저장, 수정, 삭제 시 배열이 B-Tree보다 월등히 느리므로 B-Tree를 인덱스의 자료 구조로 사용한다.
왜 보편적으로 해시 테이블 대신 B-Tree 자료 구조를 DB 인덱스로 사용하는가?
해시 테이블 내의 데이터는 정렬이 되어 있지 않으므로 부등호 연산이 불가능하다. 인덱스의 특성상 기준 값보다 크거나 작은 요소를 탐색하는 경우가 많은데, 이러한 이유로 B-Tree를 인덱스의 자료 구조로 사용한다.
그러면 해시 테이블은 인덱스에서 사용되지 않는가?
그렇지 않다. 해시 테이블은 등호 연산에는 특화되어 있으므로 해시 인덱스를 사용하는 경우도 있다. 보편적으로 잘 사용하지 않는다고 하면 맞다고 생각한다.
'스터디 > CS 스터디' 카테고리의 다른 글
| [데이터베이스] NoSQL - Why NoSQL (0) | 2022.01.03 |
|---|---|
| [데이터베이스] MySQL 트랜잭션 격리 수준 (2) | 2022.01.02 |
| [데이터베이스] MySQL 스토리지 엔진의 잠금 (0) | 2021.12.27 |
| [데이터베이스] NoSQL - What is NoSQL (0) | 2021.12.26 |
| [데이터베이스] 잠금이란? (0) | 2021.12.25 |



댓글