[BOJ] 백준 2352번 : 반도체 설계 (JAVA)
문제
반도체를 설계할 때 n개의 포트를 다른 n개의 포트와 연결해야 할 때가 있다.
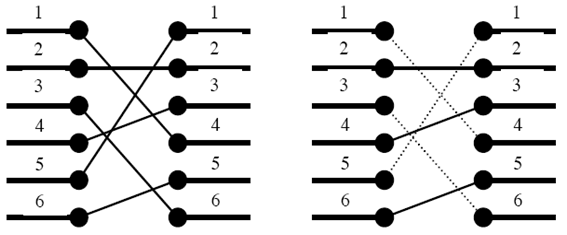
예를 들어 왼쪽 그림이 n개의 포트와 다른 n개의 포트를 어떻게 연결해야 하는지를 나타낸다. 하지만 이와 같이 연결을 할 경우에는 연결선이 서로 꼬이기 때문에 이와 같이 연결할 수 없다. n개의 포트가 다른 n개의 포트와 어떻게 연결되어야 하는지가 주어졌을 때, 연결선이 서로 꼬이지(겹치지, 교차하지) 않도록 하면서 최대 몇 개까지 연결할 수 있는지를 알아내는 프로그램을 작성하시오
입력
첫째 줄에 정수 n(1 ≤ n ≤ 40,000)이 주어진다. 다음 줄에는 차례로 1번 포트와 연결되어야 하는 포트 번호, 2번 포트와 연결되어야 하는 포트 번호, …, n번 포트와 연결되어야 하는 포트 번호가 주어진다. 이 수들은 1 이상 n 이하이며 서로 같은 수는 없다고 가정하자.
비슷한 문제
풀이
문제의 예제에서 arr = {4, 2, 6, 3, 1, 5}인 것을 알 수 있습니다. 서로 포트가 꼬이지 않으려면, {4, 6}, {2, 3, 5}처럼 증가하는 부분을 연결해야합니다. 즉, LIS 문제로 치환하여 접근할 수 있습니다.
이전 글에서 LIS에 대해서 시간 복잡도가 O(N^2)인 방식에 대해서 알아보았습니다. 하지만, 이 문제는 N의 최댓값이 40000이므로 이전 방식으로는 해결할 수 없습니다. 따라서 시간복잡도를 O(NlogN)으로 줄여야합니다. 세그먼트 트리로 하는 방식도 있지만, 저는 좀 더 이해하기 쉬운 이분탐색을 이용한 방식에 대하여 설명드리겠습니다.
로직 자체는 단순합니다.
1. 배열을 탐색하면서 큰 수를 뒤에 계속 이어 붙인다.
2. 중간에 끼어들 수 있는 수는 이분탐색을 이용하여 적절한 위치에 기존에 있던 수와 교체한다.
3. 배열을 탐색하면서 맨 앞 요소보다 작은 요소가 생기면 맨 앞 요소를 교체한다.
다만, 이 방식을 사용하면 원래 구하고자하는 가장 긴 배열의 순서와는 달라질 수 있습니다. 하지만, 길이 자체는 올바르게 구할 수 있습니다. 예제와 함께 로직이 구체적으로 어떻게 적용되는 것인지 알아보겠습니다.
예제
arr = {4, 2, 6, 3, 1, 5}
위와 같이 수열이 있다고 가정합시다.
우리는 lis라는 배열을 만들어서 arr을 탐색할 때마다 위에서 언급한 3가지 조건 중 만족하는 1가지를 적용시키면 됩니다.
처음에는 lis[0] = 4가 될 것입니다. (초기 값 설정.)

lis[0]보다 arr[1]이 작으므로 둘을 교체합니다. 즉, lis[0] = 2가 됩니다.

arr[2]은 lis[0]보다 크므로 뒤로 이어붙입시다. 즉, lis[1] = 6이 됩니다.

arr[3] = 3으로, lis에 속한 2와 6 사이에 있는 값입니다. 따라서 이분탐색을 통해서 적절한 자리에 넣어주면 됩니다.
저는 여기서 Arrays의 메소드인 binarySearch를 사용하였습니다. Arrays.binarySearch(lis, 0, idx, arr[i])와 같이 메소드를 사용하시면 됩니다.
여기서 binarySearch가 어떤 식으로 동작하는지 잠시 간단하게 알아보겠습니다.
예를 들어, arr = {2, 4, 6}이 있다고 가정합시다. 아래 표에서 빨간색은 배열에서 없는 수이고, 파란색은 배열에 존재하는 수입니다.
| 0 | 1 | 2 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| -1 | -2 | -3 | -4 |
위와 같이 binarySearch로 탐색이 가능한 수는 배열에서 인덱스를 반환하고, 없는 값은 위와 같이 음수 값을 반환합니다. 이 음수 값이 나오는 기준은 아래 코드를 참조하시면 되겠습니다.
<Arrays.binarySearch 소스 코드>
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public static int binarySearch(int[] a, int fromIndex, int toIndex, int key) {
rangeCheck(a.length, fromIndex, toIndex);
return binarySearch0(a, fromIndex, toIndex, key);
}
// Like public version, but without range checks.
private static int binarySearch0(int[] a, int fromIndex, int toIndex, int key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
int midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
|
cs |
위 코드에서 알 수 있듯이, 이분탐색을 수행하고 찾을 수 없는 곳은 -(low + 1)을 반환하게됩니다.
이 말은 -(찾고자하는 값 이상이 처음 나오는 위치 + 1)과 동치합니다. 다만, 찾고자하는 값 이상이 나오지 않을 경우, -(배열의 길이 + 1)을 반환하게 됩니다.
arr = {2, 4, 6}에서 Arrays.binarySearch(arr, 0, 3, 1}을 하게 되면, 1이라는 수는 arr에 포함되어있지않지만, arr[0] = 2는 1보다 큰 수 입니다. 따라서 "찾고자하는 값 이상이 처음 나오는 위치"는 0이 되고, 이분탐색한 결과 -1을 반환하게되는 것입니다. 이것을 흔히, lower bound라고 부릅니다.
이제, 문제로 돌아옵시다.
lis = {2, 6}인 상황이고, arr[3] = 3입니다. Arrays.binarySearch(arr, 0, 2, 3)을 하면 값이 어떻게 나올까요? 바로 -2가 됩니다. 이것을 -(-2) - 1 = 1로 가공함으로써, lis[1] = arr[3] = 3으로 교체할 수 있습니다.
즉, lis = {2, 3}으로 바뀌게 됩니다.

arr[4] = 1입니다. arr[4]는 lis[0]보다 작은 값이므로 lis[0] = 1로 바꿔줍시다.

마지막으로, arr[5] = 5입니다. lis[1]보다 큰 수이므로 뒤에 이어붙입시다.

따라서, 최대 길이는 lis의 길이인 3인 것을 알 수 있습니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < arr.length; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int[] lis = new int[N];
lis[0] = arr[0];
int idx = 1;
int tmp = 0;
for (int i = 1; i < N; i++) {
if (lis[idx - 1] < arr[i]) { // 큰 수를 뒤로 이어붙인다.
lis[idx++] = arr[i];
} else if (lis[0] > arr[i]) { // lis의 처음 수보다 작은 값을 교체한다.
lis[0] = arr[i];
} else { // lis 사이의 들어갈 수 있는 값은 이분탐색을 통해 적당한 위치에 넣어준다.
tmp = Arrays.binarySearch(lis, 0, idx, arr[i]);
lis[tmp < 0 ? (-tmp - 1) : tmp] = arr[i];
}
}
bw.write(idx + "\n");
bw.flush();
bw.close();
br.close();
}
}
|
cs |
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 17472번 : 다리 만들기 2 (JAVA) (0) | 2020.06.08 |
|---|---|
| [BOJ] 백준 9935번 : 문자열 폭발 (JAVA) (0) | 2020.06.07 |
| [BOJ] 백준 11053번 : 가장 긴 증가하는 부분 수열 (JAVA) (2) | 2020.06.06 |
| [BOJ] 백준 10451번 : 순열 사이클 (JAVA) (0) | 2020.06.05 |
| [BOJ] 백준 1181번 : 단어 정렬 (JAVA) (0) | 2020.06.04 |



댓글