[BOJ] 백준 2553번 : 마지막 팩토리얼 수 (JAVA)
문제
N!의 값을 계산한 후에, 0이 아닌 가장 낮은 자리 수를 구하시오.
예를 들어, 4! = 24 이기 때문에, 0이 아닌 가장 낮은 자리 수는 4이다. 또, 5! = 120이기 때문에, 0이 아닌 가장 낮은 자리 수는 2 이다.
입력
첫째 줄에 N이 주어진다. N은 20,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 N!의 0이 아닌 마지막 자리수를 출력한다.
풀이
팩토리얼을 이용하여 풀 수 있는 문제였습니다.
만약, 마지막 팩토리얼 수가 단순히 맨 오른쪽 자리(Unit Digit)라면, 어느 순간부터 Unit Digit은 0이 될 것입니다. 하지만, 문제에서 마지막 팩토리얼 수는 0이 아닌 가장 오른쪽 자리수라고 하였으므로 우리는 어떤 수의 끝 자리에 0이 생기지 않도록 하기 위하여 계산 과정에서 5와 2를 같은 수만큼 제거해야합니다. 일단, 묻지도 따지지도 말고 N이 15일 때 마지막 팩토리얼 수를 구하는 과정을 한 번 보시길 바랍니다.
먼저, 아래와 같이 5개씩 끊어서 곱합니다.

그리고 5의 배수를 모두 맨 앞으로 보냅니다.
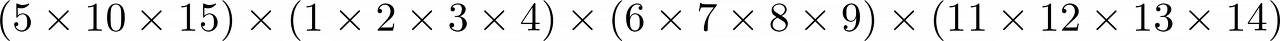
그리고 5의 배수끼리 모인 곳을 5a X b! 형태로 만들어 줍니다.

이제 4개씩 묶인 곳을 봅시다. 계산을 해 보면, 이들의 Unit Digit은 모두 4가 나온다는 것을 알 수 있습니다. 따라서, 식은 아래와 같이 바뀝니다.
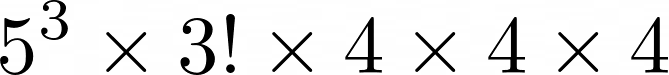
이 식을 이제, 2와 5를 소거하기 위하여 아래와 같이 바꾸겠습니다.

여기서 5와 2를 묶어서 10의 제곱 꼴로 만들어 줍니다.

10의 제곱 꼴은 마지막 팩토리얼 수를 구하는데 필요가 없으므로 이제 지워도 무방합니다.

따라서 식은 이제, 2A x A! 형태로 남게 됩니다. 그리고 이것의 Unit Digit이 우리가 구하려는 마지막 팩토리얼 수가 됩니다.
여기서 중요한 사실은 A가 N을 5로 나눈 몫이라는 것입니다. 즉, N이 5의 배수일 경우 N!의 마지막 팩토리얼 수를 구하는 것이 아니라, 2A x A!의 Unit Digit을 구하는 문제로 바뀝니다! (정확히 공식이 이렇게 되는 이유는 아래에서 더 자세히 설명하겠습니다.)
그리고 이마저도 우리가 dp를 통하여 캐싱을 한다면, A! 대신 dp[A]를 구하고, 2의 제곱 꼴도 Unit Digit으로 표현하면 답을 빠르게 구할 수 있습니다.
여기서 2의 제곱 꼴의 Unit Digit을 구하는 과정을 조금 주목해야합니다. 나열을 해 보면, {2, 4, 8, 6, ... }이 반복된다는 사실을 알 수 있고, 2(p % 4)를 통하여 Unit Digit을 도출할 수 있습니다.
다만, p가 4가 아닌 4의 배수일 경우 4로 나누었을 때 나머지가 0이 되어 Unit Digit이 1이 나오므로 24일 때의 Unit Digit인 6과 다르지 않냐고 의문을 제기할 수 있습니다. 하지만, 우리는 마지막 팩토리얼 수만 구하면 되므로 연산 과정에서 1이든 6이든 상관이 없습니다. 왜 6은 Unit Digit을 구하는 연산에서 의미가 없을까요? 그것은 짝수의 Unit Digit과 6을 곱해도 결과는 짝수의 Unit Digit이 나오기 때문입니다. 실제로 2, 4, 6, 8에 6을 곱해도 모두 Unit Digit은 2, 4, 6, 8이 나온다는 것을 알 수 있습니다.
예를 들어, N이 20이라면, 20!이 아닌 24 x 4!로 형태가 바뀌는데, 24의 Unit Digit은 6이 되고 4! 안에 짝수가 존재하므로 서로 곱하면 되는 것입니다.
여기까지 N이 5의 배수일 때 마지막 팩토리얼 수를 구하는 방법에 대해서 알아 보았습니다. 그렇다면, N이 5이상이고, 5의 배수가 아닐 때는 어떻게 마지막 팩토리얼 수를 구할 수 있을까요?
그것은 어렵지 않습니다. N보다 작은 최대 5의 배수(before)를 구한 뒤 아래와 같이 계산하면 됩니다.

가령, N이 12일 경우, 12 x 11 x 10!의 마지막 팩토리얼 수를 구하는 것이죠. 이때, 10!의 Unit Digit은 2A x A! 공식을 사용하여 짝수의 값으로 바꿀 수 있으므로, 나머지 값에 대해서는 Unit Digit만 서로 곱하면 됩니다. 10!의 Unit Digit은 8이므로 '2 x 1 x 8 => 6'이 12!의 마지막 팩토리얼 수임을 알 수 있습니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
N이 5의 배수일 때, 마지막 팩토리얼 수가 2A x A!이 되는 이유
위 풀이에서는 N이 15일 때의 예시를 가지고 공식을 도출해서 많이 부실합니다. 이제, 왜 공식이 이렇게 되는지 자세히 증명해 보겠습니다.
먼저, A! 부분을 증명해 보겠습니다. 이 부분은 어렵지 않습니다. N이 5의 배수일 경우, 곱하는 영역을 5개씩 차례대로 반드시 묶을 수 있습니다. 그런 다음 5의 배수를 앞으로 빼고, 5의 배수끼리 곱한 식을 아래와 같이 표현이 가능합니다.

팩토리얼은 2의 개수가 5의 개수보다 많은 것은 자명하므로 5의 제곱 꼴은 나중에 2의 제곱 꼴과 만나서 어차피 지워지므로 A!만 남게 됩니다.
이제, 2의 제곱 꼴을 증명하겠습니다. 위의 과정처럼 5의 배수로 앞으로 빼내고 나면, 묶은 영역의 요소가 4개가 됩니다. 그리고 이들의 Unit Digit은 항상 4로 표현이 가능합니다.
4개의 요소로는 {1, 2, 3, 4}, {6, 7, 8, 9}, ...로, 5의 배수를 제외하고 4개씩 묶입니다. 우리는 어차피 Unit Digit을 구해야하므로 십의 자리의 수는 볼 필요가 없습니다. 따라서, {1, 2, 3, 4}의 원소를 곱한 Unit Digit과 {6, 7, 8, 9}의 원소를 곱한 Unit Digit을 구하면 되는데, 둘 다 4가 됩니다.
이때, 이러한 Unit Digit이 4인 영역은 A개만큼 존재하고, 앞으로 뺀 5도 A개만큼 존재합니다. 따라서, 남는 값은 2A x A!가 됩니다. (단, A = N / 5)
참고 자료
Last non-zero digit of a factorial - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 12852번 : 1로 만들기 2 (JAVA) (5) | 2021.01.20 |
|---|---|
| [BOJ] 백준 7453번 : 합이 0인 네 정수 (JAVA) (0) | 2021.01.18 |
| [BOJ] 백준 13904번 : 과제 (JAVA) (0) | 2021.01.13 |
| [BOJ] 백준 1461번 : 도서관 (JAVA) (0) | 2020.11.27 |
| [BOJ] 백준 6219번 : 소수의 자격 (JAVA) (3) | 2020.11.13 |



댓글