[BOJ] 백준 17406번 : 배열 돌리기 (JAVA)
https://www.acmicpc.net/problem/17406
17406번: 배열 돌리기 4
크기가 N×M 크기인 배열 A가 있을때, 배열 A의 값은 각 행에 있는 모든 수의 합 중 최솟값을 의미한다. 배열 A가 아래와 같은 경우 1행의 합은 6, 2행의 합은 4, 3행의 합은 15이다. 따라서, 배열 A의
www.acmicpc.net
문제
크기가 N×M 크기인 배열 A가 있을때, 배열 A의 값은 각 행에 있는 모든 수의 합 중 최솟값을 의미한다. 배열 A가 아래와 같은 경우 1행의 합은 6, 2행의 합은 4, 3행의 합은 15이다. 따라서, 배열 A의 값은 4이다.

배열은 회전 연산을 수행할 수 있다. 회전 연산은 세 정수 (r, c, s)로 이루어져 있고, 가장 왼쪽 윗 칸이 (r-s, c-s), 가장 오른쪽 아랫 칸이 (r+s, c+s)인 정사각형을 시계 방향으로 한 칸씩 돌린다는 의미이다. 배열의 칸 (r, c)는 r행 c열을 의미한다.
예를 들어, 배열 A의 크기가 6×6이고, 회전 연산이 (3, 4, 2)인 경우에는 아래 그림과 같이 회전하게 된다.

회전 연산이 두 개 이상이면, 연산을 수행한 순서에 따라 최종 배열이 다르다.
다음은 배열 A의 크기가 5×6이고, 회전 연산이 (3, 4, 2), (4, 2, 1)인 경우의 예시이다.

배열 A에 (3, 4, 2), (4, 2, 1) 순서로 연산을 수행하면 배열 A의 값은 12, (4, 2, 1), (3, 4, 2) 순서로 연산을 수행하면 15 이다.
배열 A와 사용 가능한 회전 연산이 주어졌을 때, 배열 A의 값의 최솟값을 구해보자. 회전 연산은 모두 한 번씩 사용해야 하며, 순서는 임의로 정해도 된다.
풀이
전형적인 구현 문제였습니다. 문제에서 요구하는 대로 회전을 하고, 그 과정을 코드로 옮기시는 것이 전부였습니다. 다만, 저는 머리 속에서는 어떻게 풀어야할 지 알았는데 그것을 구현하는 것이 어려웠습니다. 또, 입력받은 순서대로 배열을 돌리는 것이 무조건 최소는 아니라서 순열을 이용하여 모든 순서에 대해서 회전을 해야했습니다.
이때, 한 번 정해진 순서에 대해서 회전을 하면 배열의 원본이 바뀌기때문에 배열은 원상복구하는 과정을 수행하였습니다.
전반적인 로직은 '순열을 통한 순서 정함 -> 회전 -> 최솟값 파악 -> 배열 원상복구'이었습니다.
순열에 대해서는 아래 사이트를 참조하시면 좋습니다.
https://yabmoons.tistory.com/100
[ 순열과 조합 구현 ] - 재귀를 통한 구현(2 - 순열) (C++)
이번 글은 저번 글에 이어서 순열에 대한 설명이다 ! ( 저번 글 바로가기 ) 기본적인 설명은 지난 글에서 모두 했으니 이번 글에서는 바로 순열 구현하는 것으로 들어가도록 하겠다. [ 구현방법 ]
yabmoons.tistory.com
최솟값 파악과 배열의 원상복구 과정은 아래 소스코드를 통해 충분히 이해하실 것이지만, 회전에 대한 부분은 따로 자세하게 설명드리겠습니다.
회전에 대한 풀이
다른 분들은 보통 특정값을 넣고, 마지막에 빼는 과정을 이용하셨지만, 저는 그것을 생각하지 못해서 비교적 비효율적이면서도 코드로 짜기 어려운 로직을 생각하였습니다. 이런 풀이도 있구나라는 생각으로 접근해 주시면 감사하겠습니다.
먼저, 다음과 같은 배열을 예시로 들겠습니다.

그리고 회전 연산의 순서가 (3, 4, 2)라고 합시다.
시작점은 (1, 2)이고, 끝점은 (5, 6)이므로 회전에 해당하지 않는 부분은 잠시 지우겠습니다.

먼저, 가장 바깥쪽 부분부터 회전해야하므로 빨간색으로 표시하겠습니다.

빨간색 영역을 시계 방향으로 1칸씩 밀면 아래와 같은 모습일 것입니다.

시작점이 기존의 2에서 8로 바뀌어야하기때문에 저는 2 아래에 있는 8부터 8, 2, 3, 2, 5를 하나로 묶었습니다. 그리고 이것은 첫 번째 줄에서 해당합니다.
첫 번째 줄 5칸이 다 찼기때문에 그 다음부터는 6, 3, 5, 1을 하나로 묶습니다. 오른쪽 세로줄을 보면 5, 6, 3, 5, 1이기때문에 올바르게 묶은 것이지요. 마찬가지로 2, 1, 4, 3과 2, 4, 3을 묶고, 여태까지 묶은 4개의 쌍을 원래 배열에 다시 대입해 주면 회전이 끝납니다.
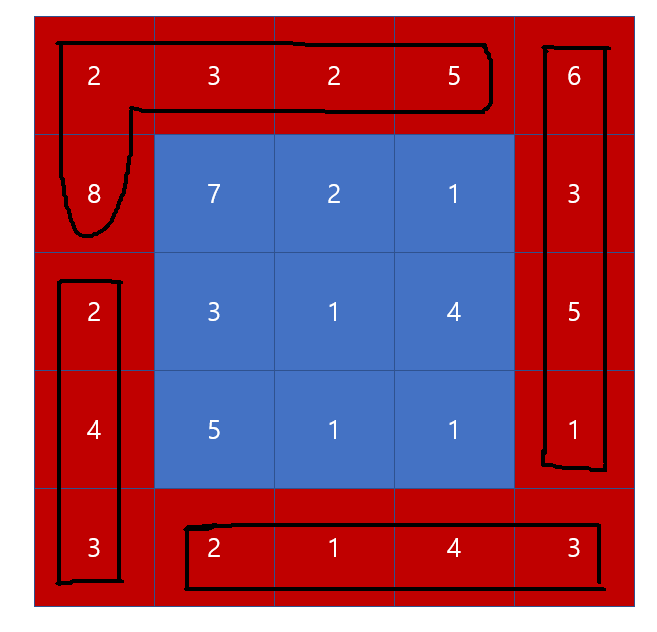
위 과정을
7 2 1
3 1 4
5 1 1
에 대해서도 반복하면 됩니다. 단, 가운데 1은 사각형 1개기때문에 수행하지 않습니다.
(3, 7, 2), (1, 4), (1, 1), (5) 4가지를 묶은 배열을 만들고, 이에 대해서 원래 배열 값에 넣어주면 됩니다.
아래 소스코드는 위 풀이를 코드로 옮긴 것입니다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
|
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
import java.util.Vector;
class Point {
int r;
int c;
int s;
Point(int r, int c, int s) {
this.r = r;
this.c = c;
this.s = s;
}
}
public class Main {
static int N, M, K;
static int[][] arr;
static int[][] copyArr;
static Point[] points;
static boolean[] select;
static Vector<Point> v;
static int ans;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
arr = new int[N + 1][M + 1];
copyArr = new int[N + 1][M + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= M; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
copyArr[i][j] = arr[i][j];
}
}
points = new Point[K];
select = new boolean[K];
for (int i = 0; i < K; i++) {
st = new StringTokenizer(br.readLine());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
int s = Integer.parseInt(st.nextToken());
points[i] = new Point(r, c, s);
}
v = new Vector<>();
ans = Integer.MAX_VALUE;
backTracking(0);
bw.write(ans + "\n");
bw.flush();
bw.close();
br.close();
}
// 원래 배열로 복구
public static void init() {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
copyArr[i][j] = arr[i][j];
}
}
}
// 최솟값 구하기
public static void calMin() {
for (int i = 1; i <= N; i++) {
int total = 0;
for (int j = 1; j <= M; j++) {
total += copyArr[i][j];
}
ans = Math.min(ans, total);
}
}
// 순열
public static void backTracking(int num) {
if (num == K) {
for (int i = 0; i < v.size(); i++) {
spin(v.get(i));
}
calMin();
init();
return;
}
for (int i = 0; i < K; i++) {
if (select[i]) {
continue;
}
select[i] = true;
v.add(points[i]);
backTracking(num + 1);
v.remove(v.size() - 1);
select[i] = false;
}
}
// 회전
public static void spin(Point p) {
int r = p.r;
int c = p.c;
int s = p.s;
while (s > 0) {
int i = r - s;
int[][] copy = new int[4][50];
copy[0][0] = copyArr[i + 1][c - s];
int idx = 1;
// 북쪽 가로줄
for (int j = c - s; j < c + s; j++) {
copy[0][idx++] = copyArr[i][j];
}
idx = 0;
// 서쪽 세로줄
for (int k = r - s; k < r + s; k++) {
copy[1][idx++] = copyArr[k][c + s];
}
idx = 0;
// 남쪽 가로줄
for (int n = c - s + 1; n <= c + s; n++) {
copy[2][idx++] = copyArr[r + s][n];
}
idx = 0;
// 서쪽 세로줄
for (int l = r - s + 2; l <= r + s; l++) {
copy[3][idx++] = copyArr[l][c - s];
}
// copy 배열에 남은 북, 동, 남, 서 영역을 copyArr으로 옮긴다.
for (int x = c - s; x <= copy[0].length + c - s; x++) {
if (copy[0][x - (c - s)] == 0) {
break;
}
copyArr[i][x] = copy[0][x - (c - s)];
}
for (int y = r - s + 1; y <= copy[1].length + r - s; y++) {
if (copy[1][y - (r - s + 1)] == 0) {
break;
}
copyArr[y][c + s] = copy[1][y - (r - s + 1)];
}
for (int w = c - s; w < copy[2].length + c - s; w++) {
if (copy[2][w - (c - s)] == 0) {
break;
}
copyArr[r + s][w] = copy[2][w - (c - s)];
}
for (int z = r - s + 1; z <= copy[3].length + r - s; z++) {
if (copy[3][z - (r - s + 1)] == 0) {
break;
}
copyArr[z][c - s] = copy[3][z - (r - s + 1)];
}
s--;
}
}
}
|
cs |
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 17471번 : 게리멘더링 (JAVA) (0) | 2020.05.26 |
|---|---|
| [BOJ] 백준 2331번 : 반복수열 (JAVA) (0) | 2020.05.25 |
| [BOJ] 백준 17070번 : 파이프 옮기기 1 (JAVA) (0) | 2020.05.23 |
| [BOJ] 백준 15954번 : 인형들 (JAVA) (0) | 2020.05.22 |
| [BOJ] 백준 1797번 : 균형잡힌 줄서기 (JAVA) (0) | 2020.05.21 |



댓글