[HackerRank] Lily's Homework (JAVA)
문제
Whenever George asks Lily to hang out, she's busy doing homework. George wants to help her finish it faster, but he's in over his head! Can you help George understand Lily's homework so she can hang out with him?
Consider an array of n distinct integers, arr = [a[0], a[1], ... , a[n - 1]]. George can swap any two elements of the array any number of times. An array is beautiful if the sum of |arr[i] - arr[i - 1]| among 0 < i < n is minimal.
Given the array arr, determine and return the minimum number of swaps that should be performed in order to make the array beautiful.
For example, arr = [7, 15, 12, 3]. One minimal array is [3, 7, 12, 15]. To get there, George performed the following swaps:

It took 2 swaps to make the array beautiful. This is minimal among the choice of beautiful arrays possible.
입력
The first line contains a single integer, n, the number of elements in arr. the second line contains n sapce-separated integers arr[i].
제한
1 <= n <= 106
1 <= arr[i] <= 2 X 109
풀이
정렬을 이용하여 풀 수 있는 문제였습니다.
이 문제를 풀기 전에 beautiful한 상태는 무엇인지 파악해야합니다. 여기서 beautiful한 상태는 인접한 요소의 차의 절댓값을 모두 더한 값이 최소일 때를 말합니다. 그리고 직관적으로는 이것이 오름차순이든 내림차순이든 정렬된 상태임을 알 수 있습니다. 이것을 증명하는 방법은 아래에 적어두었습니다.
따라서, 원래 배열에서 오름차순 배열로 만들기 위해 스왑한 횟수와 내림차순 배열로 만들기 위해 스왑한 횟수 중 더 작은 값을 답으로 도출하면 됩니다.
그렇다면, 스왑한 횟수를 어떻게 구할 수 있을까요? 이것을 알기 위해서는 정렬에서의 cycle을 알아둘 필요가 있습니다.
사이클은 어렵지 않습니다. 아래 사례 몇 가지를 봅시다.
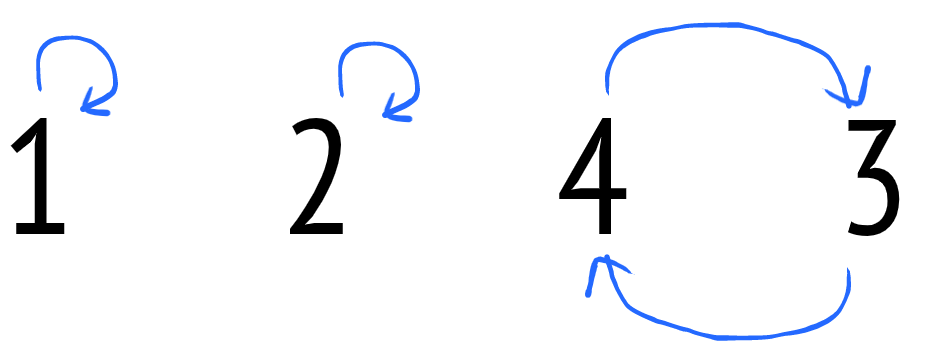
1과 2는 자기 자리에 있고, 4는 3으로 3은 4로 가야 오름차순으로 정렬이 완료됩니다.
이때, 3과 4사이의 사이클이 발생합니다.

1은 자기 자리에 있고, 4는 3으로 2는 4로, 3은 2로 가야 오름차순 정렬이 완료됩니다.
이때, 4와 2, 3사이의 사이클이 발생합니다.
그리고 사이클의 길이는 화살표, 즉 경로의 개수와 같습니다. "1 4 2 3"의 경우 사이클의 길이는 3이 되는 것입니다. 그렇다면, 사이클과 스왑은 무슨 관계가 있길래 사이클 이야기를 한 것일까요?
그것은 (사이클의 길이) - 1이 스왑 횟수이기때문입니다. 만약, 길이가 n인 사이클이 있을 때, 정렬이 되도록 (n - 2)번 스왑하면 2개의 요소만이 남는데, 이 상황에서 1번만 스왑을 하면 정렬이 완료됩니다. 따라서 (n - 1)번을 스왑하여 정렬된 상태로 만들 수 있습니다.
그리고 이 스왑의 횟수를 구하기 위해서 선택 정렬을 사용합니다. 왜 선택 정렬을 통하여 해결할 수 있는 것일까요? 이것도 내용상 길이가 조금 있어서 아래에 적어두었습니다.
선택 정렬을 통하여 문제를 해결할 수 있는데, 문제는 시간복잡도가 O(N2)라는 것입니다. 우리는 어차피 어떠한 요소를 효율적으로 정렬하는 것이 아니라 단순히 스왑 횟수만 구하면 장땡이므로, 조금 편법을 쓰면 O(NlogN)으로 줄일 수 있습니다.
선택 정렬이 오래 걸리는 이유는 다름 아닌 탐색때문입니다. 배열의 요소를 하나 하나 찾아보면서 가장 작은 수를 찾아야하므로 시간 복잡도가 O(N)이고, 스왑할 장소를 찾는 데 시간 복잡도가 O(N)입니다. 스왑할 장소를 찾는 것을 대체할 방법은 없지만, 작은 수를 찾아내는 것은 어렵지 않습니다.
바로, 원래 배열의 원소에 대해서 map에 저장해 두는 것이죠. key는 요소의 값을 value에는 인덱스를 넣어두면 됩니다. 그리고 key를 오름차순 혹은 내림차순으로 정렬하고, iterator을 이용하여 첫 번째 key부터 탐색하면, 탐색에 걸리는 시간 복잡도를 O(logN)으로 줄일 수 있습니다. 참고로, key를 정렬하기 위하여 java의 TreeMap을 사용할 것인데, TreeMap에서 get 메소드의 시간복잡도는 O(1)이 아니라 O(logN)입니다.
그리고 편법(?)을 쓴 선택 정렬을 진행하면서 스왑이 발생할 때마다 스왑한 횟수를 카운팅해 주고, 위치를 갱신해 주면 됩니다. 가령, "2 3 5 1"에서 2와 1의 위치를 스왑할 것인데, map에 있는 엔트리 {2, 0}을 {2, 3}으로 갱신해 주어야 합니다.
이것만 조심하면 충분히 구현하실 수 있을 것입니다. 아래는 위 내용을 정리한 소스코드입니다.
소스코드
Beautiful한 상태는 정렬이다. - 직관적 증명
먼저, 정렬된 상태를 생각해 봅시다. 저는 편의상 요소의 값을 막대 그래프로 나타내 보겠습니다.

여기서 인접한 요소의 차는 검은색 화살표에 속하고, 이들을 모두 더한 것은 빨간색 화살표에 해당합니다.
만약, 이렇게 정렬된 상태가 아닌 중간에 대소 관계가 깨지는 경우를 생각해 보겠습니다.

한 눈에 봐도 검은색 화살표의 길이 합이 빨간색 화살표의 길이보다 크다는 것을 알 수 있습니다. 이것은 첫 번째 막대와 두 번째 막대에서 구한 길이와 두 번째 막대와 세 번째 막대에서 구한 길이에서 중복이 발생하였기때문입니다.
따라서 길이의 중복이 없는 정렬된 상태이어야 beautiful한 상태가 됩니다.
Beautiful한 상태는 정렬이다. - 귀납적 증명
길이가 n인 배열이 "beautiful"하고, "정렬된" 상태라면, 새로운 요소를 "정렬된" 상태를 유지하는 방향으로 추가했을 때, 생성되는 새로운 배열은 "beautiful"하다고 가정해보겠습니다.
base는 n = 2일 때이고, 이것은 그 자체로 정렬되었으며 beautiful합니다.
이때, 길이가 k인 배열이 위 가정을 만족한다고 해 봅시다. 그리고 길이가 (k + 1)인 배열도 위 가정을 만족하는지 검증해 보기 위하여 어떠한 요소 c를 배열에 첨가합시다.
첫 번째 케이스는 k개의 배열 안에 A, B (A < B)가 있는데, 정렬 조건을 만족하도록 A와 B 사이에 C를 넣는 상황입니다. 이때, A와 B, C에 대해 인접한 요소의 차의 합을 구하면 (C - A) + (B - C) = B - A가 됩니다.
두 번째 케이스는 k개의 배열 안에 A, B (A < B)가 있는데 정렬 조건을 만족하지 않고 C를 넣는 상황입니다. 여기서도 2가지 경우로 나뉘는데, A > C < B 즉, C < A < B가 되도록 C를 첨가하는 경우를 생각해 봅시다.
이때, A와 B, C에 대해 인접한 요소의 차의 합을 구하면, (A - C) + (B - C) = A + B - 2C가 됩니다.
저는 첫 번째 케이스가 더 작다고 가정한 것이므로 B - A < A + B - 2C가 맞는지 보이면 됩니다. 적절히 이항을 하고 정리를 하면, A - C > 0인데, C < A < B라고 두 번째 케이스에서 전제를 하였으므로 제가 내린 가정에 부합합니다.
이번에는 정렬 조건을 만족하지 않고 C를 넣되, A < C > B 즉, A < B < C가 되도록 C를 첨가해 봅시다.
이때, A와 B, C에 대해 인접한 요소의 차의 합을 구하면, (C - A) + (C - B) = 2C - A - B가 됩니다.
저는 첫 번째 케이스가 더 작다고 가정한 것이므로 B - A < 2C - A - B가 맞는지 보이면 됩니다. 적절히 이항을 하고 정리를 하면, C - B > 0인데, A < B < C라고 두 번째 케이스에서 전제를 하였으므로 제가 내린 가정에 부합합니다.
따라서, 수학적 귀납법에 의하여 길이가 n인 배열이 "beautiful"하고, "정렬된" 상태라면, 새로운 요소를 "정렬된" 상태를 유지하는 방향으로 추가했을 때, 생성되는 새로운 배열은 "beautiful"합니다.
선택 정렬을 사용한 이유
스왑 횟수를 구하는 데 선택 정렬을 사용한 이유는 간단합니다. 이 정렬은 해당 배열의 사이클을 해치지 않기 때문이죠.
예를 들어 배열의 요소가 2, 5, 3, 1이라고 해 봅시다. 그렇다면 1은 2로 가야하고, 2는 5로 가야하고, 5는 3으로 가야하고, 3은 제 자리에 있어야하므로 길이가 3인 사이클이 발생합니다. 그리고 선택 정렬에 의하여 1은 2로 가야합니다.
이제, 배열이 1, 5, 3, 2로 바뀌었습니다. 1을 제외하고 5, 3, 2만 보면 됩니다. 5는 2로 가야하고, 3은 제자리에, 2는 5로 가야하므로 길이가 2인 사이클이 발생합니다. 그리고 선택 정렬에 의하여 2는 5로 가야합니다.
마지막으로, 배열이 1, 2, 3, 5로 바뀌었고, 이것은 정렬된 상태이므로 선택 정렬 작업을 종료합니다. 보시다시피, 요소가 2, 5, 3, 1인 배열은 사이클의 길이가 3이므로 스왑은 2번 이루어져야합니다. 이때, 선택 정렬은 원래 가야하는 사이클의 경로대로 가면서 스왑도 2번 이루어졌습니다.
따라서, 선택 정렬을 이용하여 최소의 스왑 횟수를 구할 수 있습니다.
참고 사이트
Lily's Homework · Coding Gym
coding-gym.org
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > HackerRank' 카테고리의 다른 글
| [HackerRank] Pairs (JAVA) (0) | 2021.01.09 |
|---|---|
| [HackerRank] Jim and the Orders (JAVA) (2) | 2021.01.06 |
| [HackerRank] Forming a Magic Square (JAVA) (0) | 2020.12.29 |
| [HackerRank] The Power Sum (JAVA) (0) | 2020.12.28 |



댓글