[BOJ] 백준 9576번 : 책 나눠주기 (JAVA)
문제
백준이는 방 청소를 하면서 필요 없는 전공 서적을 사람들에게 나눠주려고 한다. 나눠줄 책을 모아보니 총 N권이었다. 책이 너무 많기 때문에 백준이는 책을 구분하기 위해 각각 1부터 N까지의 정수 번호를 중복되지 않게 매겨 두었다.
조사를 해 보니 책을 원하는 서강대학교 학부생이 총 M명이었다. 백준이는 이 M명에게 신청서에 두 정수 a, b (1 ≤ a ≤ b ≤ N)를 적어 내라고 했다.
그러면 백준이는 책 번호가 a 이상 b 이하인 책 중 남아있는 책 한 권을 골라 그 학생에게 준다. 만약 a번부터 b번까지의 모든 책을 이미 다른 학생에게 주고 없다면 그 학생에게는 책을 주지 않는다.
백준이가 책을 줄 수 있는 최대 학생 수를 구하시오.
입력
첫째 줄에 테스트 케이스의 수가 주어진다.
각 케이스의 첫 줄에 정수 N(1 ≤ N ≤ 1,000)과 M(1 ≤ M ≤ 1,000)이 주어진다. 다음 줄부터 M개의 줄에는 각각 정수 ai, bi가 주어진다. (1 ≤ ai ≤ bi ≤ N)
출력
각 테스트 케이스마다 백준이가 책을 줄 수 있는 최대 학생 수를 한 줄에 하나씩 출력한다.
풀이
그리디 알고리즘으로 해결할 수 있는 문제였습니다.
1 ~ N번까지 총 N개의 책이 주어지고, a부터 b까지의 범위 안에 해당하는 책 아무거나 학생에게 나누어주는 방식의 문제입니다. 이 때, 범위가 서로 겹치는 경우를 잘 고려해서 최대로 학생에게 책을 나누어 주는 것이 핵심이었습니다.
그리디 알고리즘은 자료를 정렬하는 방식을 많이 쓰기 때문에 이 문제에도 많이 적용하려고 할 것입니다.
저는 일단 아무 생각 없이 a를 오름차순 정렬하고, a가 같을 경우 b에 대해 오름차순 정렬해 보았습니다.
그리고 정렬한 각각의 범위 내에서 가능한 작은 번호의 책을 나누어 주는 방식으로 로직을 세웠습니다.
대충 여러 가지 예시가 맞아서 제출했는데 당연히 틀렸습니다.
반례는 아래와 같습니다.
1 2
1 3
2 2
만약 1 ~ 3번까지의 책이 있고, 제가 세운 기준으로 정렬을 하면 위와 같을 것입니다.
처음에는 1번 책을 주고, 그 다음에는 2번 책을 주기 때문에, 총 2명의 학생에게만 책을 줄 수 있습니다.
하지만, 실제로는 3권이 가능합니다. 아래처럼 정렬하면 말이죠.
1 2
2 2
1 3
즉, a가 아니라 b에 대해 오름차순 정렬해야하고, b가 같을 경우 a에 대해 오름차순 정렬하는 방식으로 기준을 바꿔야 합니다.
그리고 위와 동일하게 각각의 범위 내에서 가능한 작은 번호의 책을 주는 것이죠.
이렇게 하면 최대한 많은 학생에게 책을 줄 수 있게 됩니다.
그렇다면, 왜 b에 대해 오름차순 정렬해야 최대한 많은 학생에게 책을 줄 수 있을까요?
수식적으로 증명은 모르겠으나, 아래 그림을 보면 직관적으로 이해가 가실 겁니다.
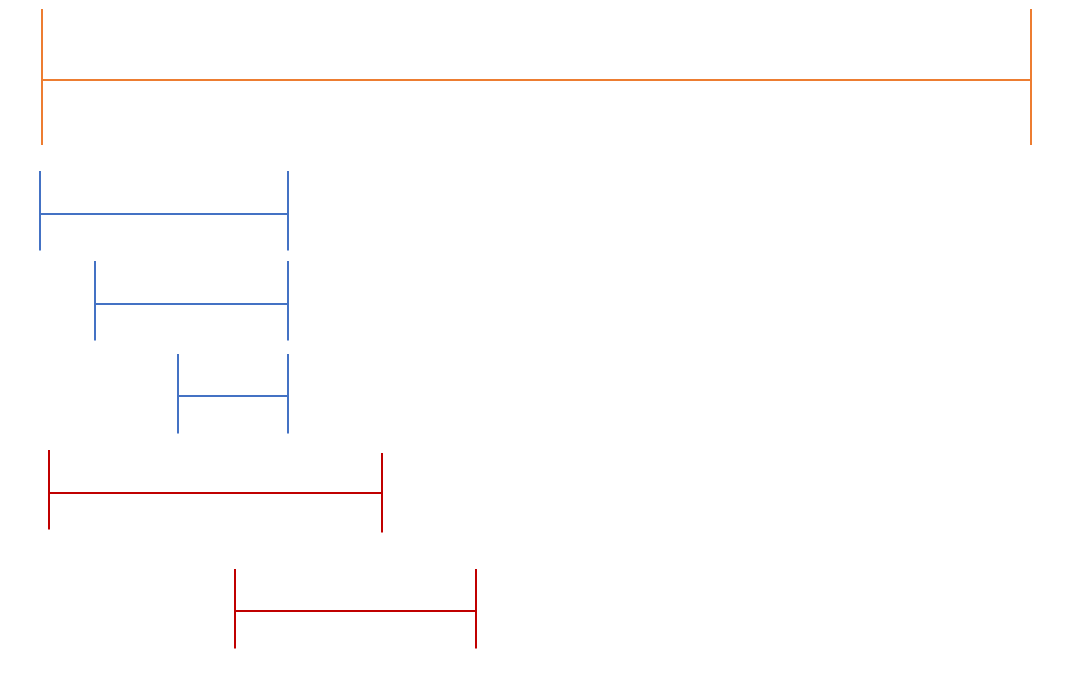
맨 위에 긴 주황 선은 전체 1 ~ N번까지의 전체 범위를 나타냅니다. 이 부분은 실제로 입력값으로 주어진 범위는 아닙니다.
실제로, "a b"와 같이 입력값으로 주어진 부분은 아래 파란색과 빨간색 선으로 이루어진 범위입니다.
가능한 작은 범위의 책을 준다고 하였으므로 위와 같이 정렬된 범위에서는 아래와 사진과 같이 책을 나누어 주게 될 것입니다.
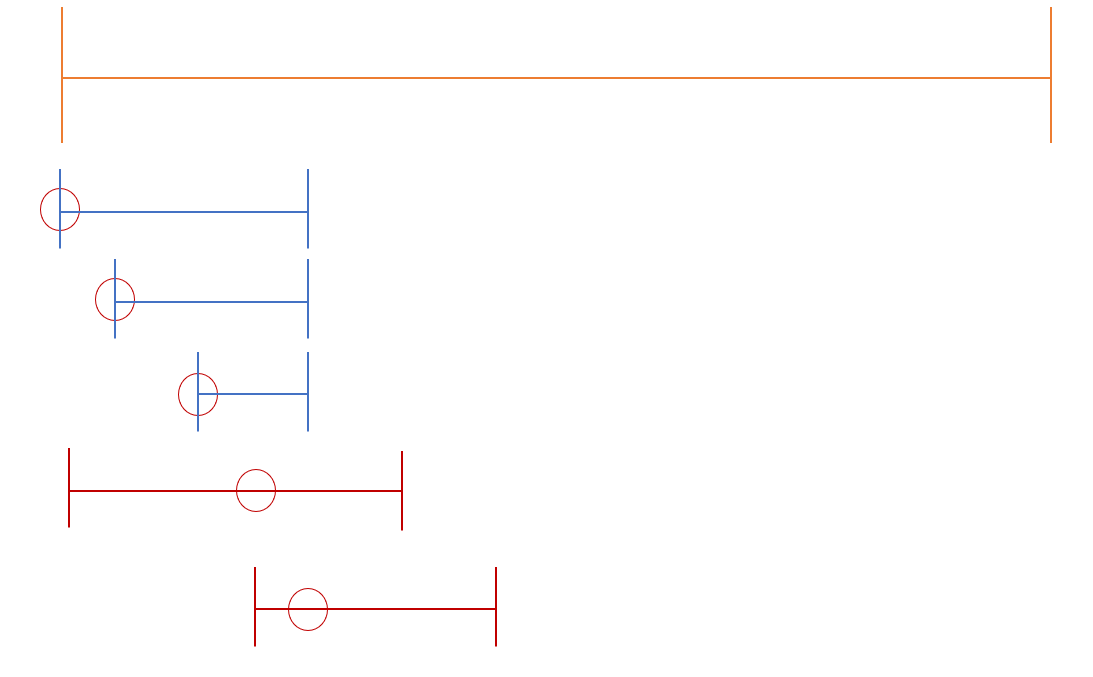
동그라미 친 부분은 각각의 영역에서 특정 책을 나누어 주었다는 뜻입니다.
그림을 보시면 아시겠지만, 가능한 가장 작은 번호부터 차례 차례 빈틈 없이 책을 나누어 주고 있는 것을 알 수 있습니다.
최선의 경우, 1번부터 N까지 모두 나누어 줄 수 있게 되는 것이죠.
이렇듯, b에 대해 오름차순 정렬하고 b가 같다면 a에 대해 오름차순함으로써 문제를 해결할 수 있습니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 9095번 : 1, 2, 3 더하기 (JAVA) (0) | 2020.10.26 |
|---|---|
| [BOJ] 백준 2109번 : 순회강연 (JAVA) (0) | 2020.10.24 |
| [BOJ] 백준 2862번 : 수학 게임 (JAVA) (0) | 2020.10.14 |
| [BOJ] 백준 2373번 : Fibonacci Game (JAVA) (0) | 2020.10.14 |
| [BOJ] 백준 13034번 : 다각형 게임 (JAVA) (0) | 2020.10.12 |



댓글