[BOJ] 백준 16884번 : 나이트 게임 (JAVA)
문제
나이트 게임은 크기가 N×N인 체스판 위에서 진행되는 게임이고, 나이트를 하나씩 턴을 번갈아가며 놓는 게임이다.
나이트는 이미 놓여져 있는 나이트가 공격할 수 있는 칸에 놓을 수 없다.
나이트를 (r, c)에 놓은 경우에는 (r-2, c+1), (r-1, c+2), (r+1, c+2), (r+2, c+1), (r+2, c-1), (r+1, c-2), (r-1, c-2), (r-2, c-1)이 공격할 수 있는 칸이다.
나이트를 놓을 수 있는 칸이 없는 사람이 게임을 지게 된다. 구사과와 큐브러버가 이 게임을 최적의 방법으로 플레이했을 때, 이기는 사람을 구하는 프로그램을 작성하시오. 게임은 구사과가 먼저 시작한다.
입력
첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 100)가 주어진다. 둘째 줄부터 T개의 줄에 테스트 케이스가 한 줄에 하나씩 주어지며, 체스판의 크기 N(1 ≤ N ≤ 10,000)으로 이루어져 있다.
출력
각각의 테스트 케이스마다 게임을 이기는 사람을 출력한다. 구사과가 이기는 경우에는 "koosaga", 큐브러버가 이기는 경우에는 "cubelover"를 출력한다.
풀이
기하학적인 개념과 게임 이론을 이용하여 풀 수 있는 문제였습니다.
우리가 흔히 알고 있는 체스의 나이트가 공격할 수 있는 8가지 방향을 가능한 모두 체크하고, 마지막에 더 이상 나이트 말을 놓을 수 없는 플레이어가 지는 규칙의 게임이었습니다.
이 문제를 풀기 위해서는 '점대칭' 개념이 필요했습니다.
점대칭은 한 도형을 한 점 주위로 180° 회전했을 때, 본래의 도형에 완전히 겹치는 대칭을 말한다.
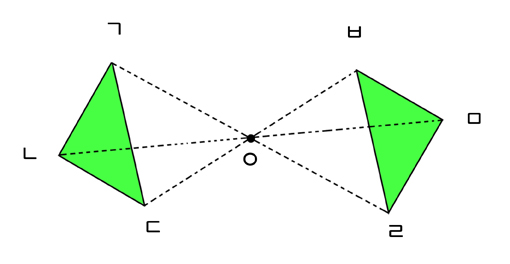
위는 점대칭을 나타내는 두 도형입니다.
뜬금없이 점대칭 이야기가 나왔지만, 이 문제에서는 점대칭을 통해 필승 전략이 아주 단순해집니다.
바로, 상대가 놓은 나이트의 위치에 해당하는 점대칭 위치에 나이트를 놓으면 됩니다.
만약, A가 i 지점에 나이트를 놓고, 공격 방향을 모두 체크했다고 가정합시다.
그렇다면, B가 i에 점대칭인 j 지점에 나이트를 놓고 공격 방향을 모두 체크하면, i 지점 및 A가 체크한 공격 방향과 모두 대칭이 됩니다.
이를 일반화하면, N이 짝수가 되면 후공이 이기고, N이 홀수가 되면 선공이 이기게 됩니다.
N이 짝수일 경우, 선공이 어디를 놓든 간에 후공은 점대칭 방향에 말을 놓으면 되므로 차례대로 턴이 진행된다면 결국 선공이 패배하게 됩니다.
반대로 N이 홀수일 경우, 선공은 한가운데 지점에 말을 놓으면 됩니다.
한가운데에는 점대칭에 해당하는 점이 없으므로 짝수의 게임판에서 다음 차례인 후공이 선공이 되어 게임을 수행하는 것과 같아집니다.
위의 내용을 기반으로 소스코드를 작성하시면 됩니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 3358번 : Towers of coins (JAVA) (0) | 2020.10.06 |
|---|---|
| [BOJ] 백준 5945번 : Treasure Chest (JAVA) (0) | 2020.10.06 |
| [BOJ] 백준 18939번 : 경비병 세우기 게임 (JAVA) (0) | 2020.10.05 |
| [BOJ] 백준 16896번 : 더일곱이 게임 (JAVA) (0) | 2020.10.04 |
| [BOJ] 백준 16876번 : 재미있는 숫자 게임 (JAVA) (0) | 2020.10.03 |



댓글