[BOJ] 백준 16897번 : 아인타 게임 (JAVA)
문제
구사과와 큐브러버는 아인타 게임을 하려고 한다. 아인타 게임은 크기가 N×M인 체스판 위에 체스말 하나를 놓고 진행하는 게임이다. 체스판 위에 놓은 체스말은 "아인타"이다.
이 체스말은 아인타가 자신을 본따서 만든 체스말로, 아래로 한 칸 또는 오른쪽으로 한 칸 이동하는 것이 가능하다. 또, 아인타에는 정수 k가 하나 적혀있는데, 오른쪽 아래 대각선 방향으로 k칸 이동할 수 있다. 즉, 아인타가 있는 곳이 (r, c) 라면, (r+1, c), (r, c+1), (r+k, c+k)가 아인타가 한 번에 이동할 수 있는 곳이다. 체스판의 밖으로 이동하는 것은 불가능하다.
가장 처음에 아인타는 가장 왼쪽 윗 칸에 있다. 두 사람은 턴을 번갈아 가지면서 아인타를 한 번씩 이동시키려고 한다. 더 이상 아인타를 움직일 수 없는 사람이 게임을 진다.
두 사람이 게임을 최적의 방법으로 진행했을 때, 누가 이기는지 구하는 프로그램을 작성하시오. 게임은 구사과가 먼저 시작한다.
입력
첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 100,000)가 주어진다. 둘째 줄부터 T개의 줄에 테스트 케이스가 한 줄에 하나씩 주어지며, 한 테스트 케이스는 K, N, M(1 ≤ K, N, M ≤ 109)으로 이루어져 있다.
출력
각각의 테스트 케이스마다 이기는 사람을 출력한다. 구사과가 이기는 경우에는 "koosaga", 큐브러버가 이기는 경우에는 "cubelover"를 출력한다.
풀이
스프라그 - 그런디 정리를 이용하여 풀 수 있는 문제였습니다.
(1, 1)에서 (N, M) 보다는 (N, M)에서 (1, 1) 로 간다고 가정하여 푸는 것이 좀 더 편했습니다.
처음에, dp[1][i][k]와 dp[i][1][k]는 1과 0 밖에 없으므로 적절히 초기화해 놓고, 오른쪽, 아래, 대각선으로 가는 경우에 대하여 그런디 수를 구하면 됩니다.
하지만, K, N, M이 최대 10억이기때문에 위와 같이 dp를 저장해서 풀면 메모리 초과가 발생합니다. 따라서 K, N, M을 약 15 정도로 설정하여 출력을 한뒤, 규칙을 찾는 것이 중요했습니다.
그런데, 규칙이 생각보다 만만치가 않았습니다. 나중에 알고 보니, 수식으로 간단하게 표현하신 분도 많았지만, 저는 지금도 그러한 로직이 생각나지 않아서 고생을 많이 했습니다.
일단, K = 1, K = 2, K = 3일 때에 대해 출력한 값들을 봅시다.
(참고로, N과 M의 인덱스는 1부터 시작한다고 가정합니다.)
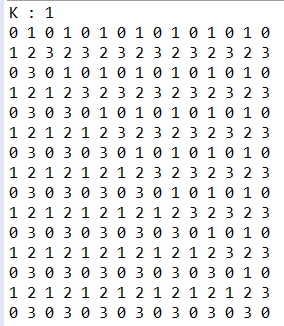

언뜻 봐도, 굉장히 난해해 보이고 규칙도 뭔가 없어 보입니다.
일단, K = 1을 살펴봅시다.
우리는 선공과 후공의 승패만 판단하면 되므로, dp[i][j][k] 의 값이 1, 2, 3 중 무엇인지가 중요한게 아니라, "dp[i][j][k] = 0 인가? 만 파악하면 됩니다.
그런 의미에서 K = 1일 때, 0인 부분은 찾기 쉽습니다. N과 M이 홀수면 0이고, 그 외에는 0이 아닙니다.
(다시 언급하자면, N과 M은 인덱스가 1부터 시작합니다.)
K = 2와 K = 3을 살펴봅시다.
이번에는 홀수 줄, 짝수 줄 구분할 것 없이 무작위로 0이 나열된 것처럼 보입니다.
하지만, 여기서 1차적인 규칙은 찾아낼 수 있었습니다.

바로 K 만큼 0과 1이 규칙성 있게 0101... 또는 1010... 으로 나열된다는 사실이었죠.
이러한 규칙을 파악하였으면, K = 2에 집중해 봅시다.

여기서, (1, 1), (2, 2), (3, 3), ... 과 같은 (i, i)에 대해 주목해야합니다.
그리고 (i, i)를 기준으로 오른쪽과 아래 방향으로 010101... 또는 232323... 또는 101010... 이 반복된다는 사실을 알 수 있습니다.
이제, (i, i)에 해당하는 그런디 수를 쭉 나열해 보겠습니다.
0, 0, 2, 1, 1, 2, 0, 0, 2, 1, 1, ...
저는 처음으로 그런디 수가 2가 되는 지점을 주목하였습니다. 그리고 그 부분은 (K + 1) 번째인 3번째에 해당하는 것을 알 수 있습니다.
앞의 0을 지우고 다시 나열하면 아래 표와 같습니다.
| G | 2 | 1 | 1 | 2 | 0 | 0 | 2 | 1 | 1 |
| Point | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
앞의 0을 제외하면 (3, 3) 일 때 그런디 수는 2, (4, 4) 일 때 그런디 수는 1, (5, 5) 일 때 그런디수는 1.. 과 같이 표현할 수 있습니다.
이 때, 잘 보면 3, 6, 9 Point는 모두 그런디 수가 2라는 점을 알 수 있습니다. 즉, (K + 1)의 배수인 지점은 그런디 수가 2이고, 그 지점에서 오른쪽과 아래쪽은 23232323... 이 반복되므로 그런디 수 0 이 존재하지 않습니다.
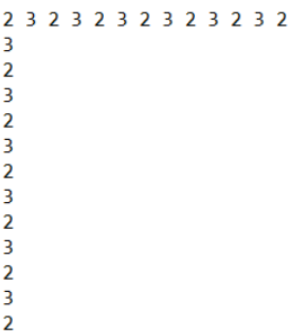
이제, 그런디 수가 0과 1인 Point를 봅시다.
2와 2 사이의 1이 K번 만큼 반복되고, 다시 2와 2사이의 0이 K번 만큼 반복됩니다.
먼저, 그런디 수가 1인 경우를 보면, Point가 4, 5, 10, 11 이라는 것을 알 수 있습니다.
그리고 각각에 대해 (K + 1)만큼 나눈 몫은 1, 1, 3, 3이 됩니다.
그런디 수가 0인 경우를 보면, Point가 7, 8, 13, 14 라는 것을 알 수 있습니다.
그리고 각각에 대해 (K + 1)만큼 나눈 몫은 모두 2, 2, 4, 4 이 됩니다.
따라서, Point를 (K + 1)로 나누어 보고, 몫이 홀수면 그런디 수가 1이고, 짝수면 그런디 수가 0임을 알 수 있습니다.

위 사진은 Point가 1일 때, 오른쪽과 아래쪽으로 10101... 이 반복되는 것을 알 수 있습니다.
여기서, N보다 M이 크다면, 짝수와 홀수 여부에 따라서 0을 골라낼 수 있을 것입니다.

위 사진은 Point가 0일 때, 오른쪽과 아래쪽으로 010101... 이 반복되는 것을 알 수 있습니다.
여기서 N보다 M이 크다면, 짝수와 홀수 여부에 따라서 0을 골라낼 수 있을 것입니다.
지금까지 꽤 긴 이야기를 하였습니다. 간단히 요약하고 나머지 case를 보도록 합시다.
우리는 K만큼 10101... , 010101... 이 반복되는 부분을 제외한 후, (K + 1, K + 1) 부터 (i, i) 를 기점으로 오른쪽과 아래쪽 숫자에 대한 규칙성을 파악하였습니다.
이 때, (i, i)에 해당하는 그런디 수가 2이면, 2323... 만 반복되므로 0인 그런디 수가 존재하지 않고, (i, i)에 해당하는 그런디 수가 0 또는 1이면, 0인 그런디 수가 존재한다고 서술하였습니다.
이제, 우리가 주목해야할 점은 (i, i)의 왼쪽 부분입니다. 이 부분이 꽤나 규칙을 찾기 어려웠습니다.

검은색 선을 기준으로 왼쪽 요소를 살펴봅시다.
딱히 0의 개수의 규칙성이 없어보입니다. 실제로, 저도 온갖 규칙을 파악하려고 노력하였으나, 마땅한 식이 보이질 않았습니다. 그래서 사고를 한 번 전환했습니다.

예를 들어, 위와 같이 (9, 9) 를 기준으로 (9, 5)의 그런디 수를 구한다고 가정합시다. 동그라미친 부분이 (9, 5) 입니다.
(K = 2 이므로 앞의 010101... 만 반복되는 구간이 존재)
우리는 위에서 열심히 (9, 9)의 오른쪽과 아래쪽만 구하는 규칙을 유도했지, 왼쪽에 대한 이야기는 전혀 없었습니다.
따라서, 역발상으로 (9, 3) 대신 (5, 5)으로 위로 쭉 올렸습니다.

빨간색으로 표시한 부분이 기존의 (9, 5)에서 (5, 5)으로 위로 올린 지점입니다.
이제, (9, 5)의 그런디 수를 구하는 일은 간단해졌습니다.
(5, 5)의 그런디 수는 위에서 언급한 방식으로 구할 수 있기때문이죠.
(5, 5)의 그런디 수는 5 / 3 = 1 이므로 1 입니다. 그리고 (5, 5) 부터 (9, 9) 까지는 총 4번의 변화가 있다는 것을 알 수 있습니다. 따라서, 1 -> 0 -> 1 -> 0 -> 1 로 변하게 되어, (9, 9)의 그런디 수는 9라고 결론지을 수 있습니다.
이제, 모든 케이스에 대한 검사가 끝났습니다.
전반적인 로직은 아래와 같습니다.
1. K = 1일 경우, 따로 예외 처리한다.
2. N 또는 M이 K 보다 작을 경우, 예외 처리한다. (010101... 만 반복되는 구간)
3. N이 M 보다 클 경우, (i, i)에 해당하는 그런디 수를 구하고, 오른쪽을 관찰한다.
4. N이 M 보다 작을 경우, (M, M)에 해당하는 그런디 수를 구하고, (M, M) 에서 (N, M) 으로 어떻게 변하는 지 관찰한다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 9655번 : 돌 게임 (JAVA) (0) | 2020.09.04 |
|---|---|
| [BOJ] 백준 18937번 : 왕들의 외나무다리 돌게임 (JAVA) (0) | 2020.09.03 |
| [BOJ] 백준 16889번 : 중복 없는 님 게임 (JAVA) (0) | 2020.09.02 |
| [BOJ] 백준 7562번 : 나이트의 이동 (JAVA) (0) | 2020.09.01 |
| [BOJ] 백준 16887번 : 루트 님 게임 (JAVA) (0) | 2020.08.31 |



댓글