[SCPC - 2019년 1차 예선] 공 굴리기 (JAVA)
문제
아래 그림에서 보인 것처럼 장애물이 놓인 길을 따라 공을 오른쪽으로 굴릴 때, 공의 중심이 어떤 궤적을 따라 이동하는지 알고자 한다.
길에 놓인 장애물들은 직사각형으로 표시되고, 모든 장애물은 x 축 상에 놓여있다.
공이 장애물을 만나 더 이상 움직일 수 없다면 그림에서 보듯이 장애물의 벽 또는 모서리를 따라 넘어가되, 공은 어떤 경우에도 장애물에서 떨어지지 않은 채 장애물의 벽 또는 모서리를 따라 구르며, 아무리 높은 장애물도 넘어 갈 수 있다.
공의 반지름, 출발점 위치(즉, 공의 중심의 x 좌표), 도착점 위치, 그리고 모든 장애물의 위치와 크기에 대한 정보가 주어질 때, 공의 중심이 이동한 총 거리를 출력하는 프로그램을 작성하고자 한다.
단, 공의 반지름을 R이라 하면, 모든 장애물의 너비는 2R 초과이며, 또한 장애물 사이의 간격도 2R 초과이다. 그리고 출발점과 도착점에서는 공이 항상 바닥에 닿아 있다고 가정하라.

입력
입력 파일에는 여러 테스트 케이스가 포함될 수 있다. 파일의 첫째 줄에 테스트 케이스의 개수를 나타내는 자연수 T 가 주어지고, 이후 차례로 T 개의 테스트 케이스가 주어진다. ( 1≤T≤150 )
각 테스트 케이스의 첫 줄에는 세 개의 정수 R ( 1≤R≤100 ) , S ( 1≤S≤1,000 ), E ( 1≤E≤1,000,000 )가 주어지는데(S≤E), R 은 공의 반지름을, S 는 공의 출발점 위치(즉, 공의 중심의 x 좌표)를, E 는 공의 도착점 위치를 나타낸다.
그 다음 줄에는 정수 N ( 1≤N≤1,000 )이 주어지는데, 이는 장애물의 개수를 나타낸다. 이어지는 N 줄의 i ( 1≤i≤N ) 번째 줄은 i 번째 장애물에 대한 정보를 나타내는 세 정수 li , ri , hi ( 1≤hi≤1,000 )가 주어지는데, 이는 각각 장애물의 왼쪽 경계의 x 좌표, 장애물의 오른쪽 경계의 x 좌표, 장애물의 높이를 나타낸다.
이 장애물은 왼쪽부터 오른쪽으로 차례로 주어진다. 출발점과 첫번째 장애물의 왼쪽 경계, 각 장애물의 왼쪽 경계와 오른쪽 경계, 마지막 장애물의 오른쪽 경계와 도착점의 거리는 2R 초과이다.
즉, 입력되는 두 x 좌표의 차이인 l1−S , r1−l1 , l2−r1 , r2−l2 , … , rN−lN , E−rN의 값은 모두 2R 초과이다.
- 점수 : 각 제출에서 취득한 점수 중에서 최대 점수(만점 150점)
주어지는 테스트 케이스 데이터들의 그룹은 아래와 같으며, 각 그룹의 테스트 케이스를 모두 맞추었을 때 해당되는 부분 점수를 받을 수 있다.
ㆍ 그룹 1 (56점) : 모든 장애물의 높이는 2R 보다 크다.
ㆍ 그룹 2 (94점) : 이 그룹의 테스트 케이스에서는 원래의 조건 외에는 다른 제약조건이 없다.
출력
각 테스트 케이스의 답을 순서대로 표준출력으로 출력하여야 하며,
각 테스트 케이스마다 첫 줄에는 “Case #C”를 출력하여야 한다. 이때 C는 테스트 케이스의 번호이다.
그 다음 줄에, 공의 중심이 이동한 거리를 계산하여 출력하여라.
절대 혹은 상대 오차가 10−610−6 이하이면 정답으로 인정한다.
따라서 소수점 아래 출력은 6자리 이상이어야 한다.
예를 들어, 답이 123.456789이면 123.456791, 123.45678900, 123.4567891012 모두 오차범위 내이기 때문에 정답으로 인정된다.
풀이
고등학교 원과 관련된 기하 문제였습니다.
장애물과 장애물 사이의 거리는 2R을 초과하므로 장애물을 겹치게 생각하지 않고, 독립적으로 판단하여도 무방하였습니다.
따라서, 장애물이 없다고 가정하여 전체 거리인 E - S를 구한 후, 장애물로 인해서 위로 올라가거나 아래로 내려간 거리를 추가로 더해주면 됩니다.
다만, 장애물의 경계면을 이동할 때, x축과 평행하게 이동하지 않고 부채꼴 형태로 이동한다는 점을 주의해야 합니다.
다시 말해서, 원래는 x축과 평행하게 이동하지만, 장애물때문에 부채꼴 형태로 이동했으므로, 이 경우의 x축 방향 거리를 빼 주어야 합니다. 이 부분은 아래 그림에서 자세히 살펴보겠습니다.
먼저, ans = E - S로 장애물이 없다고 가정하였을 때, 원의 중심이 이동한 거리로 초기화합니다.
그리고 장애물의 높이가 원의 반지름보다 크거나 같을 때와 작을 때로 케이스를 나누어서 생각해야 합니다.
1) 장애물의 높이 >= 원의 반지름
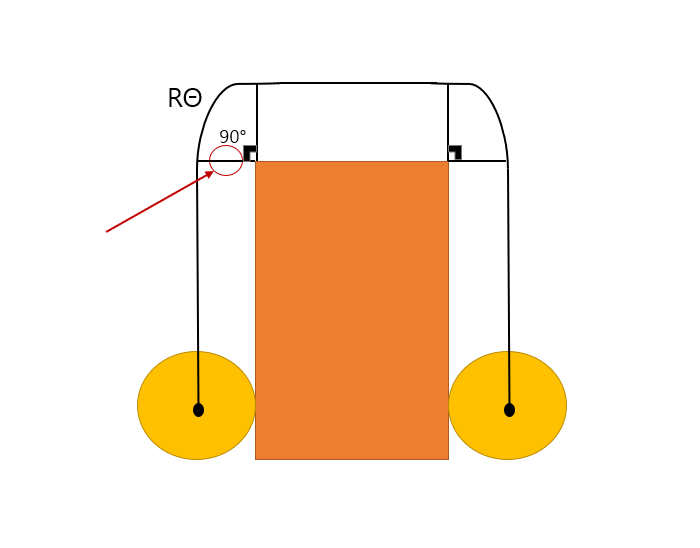
위의 검은색 선이 원의 중심이 이동한 거리입니다.
이 때, 장애물의 경계면을 넘어가는 부분이 90°이므로 부채꼴의 호의 길이는 π / 2 * R이 됩니다.
여기서, 빨간색으로 강조한 부분은 전체 거리에서 빼 주어야하는 길이입니다.
원래대로라면 저 길이만큼 앞으로 전진했을텐데, 장애물의 경계면을 넘기 위해서 저 길이 대신 부채꼴의 호의 길이를 택했기때문이죠.
따라서 오른쪽 경계면까지 포함하면, 2 * (h - R) + π / 2 * R - 2 * R 로 식을 표현할 수 있습니다.
2) 장애물의 높이 < 원의 반지름

위와 같이 장애물의 높이보다 원의 반지름이 작은 경우, 각도가 90°가 되질 않습니다.
여기서 장애물 아래 있는 원의 중심에서 수직 방향으로 아래 선을 그으면, 엇각에 의해서 Θ이 됩니다.
그리고 이 Θ를 통해서 부채꼴의 호의 길이를 구할 수 있습니다.

cosΘ는 (R - h) / R입니다. 따라서, Θ = arcos( (R - h) / R )을 통해서 구할 수 있습니다.
그리고 RΘ를 계산하여 부채꼴의 호의 길이를 구하면 됩니다.
반면, 화살표로 강조한 거리는 장애물이 없었다면 이동했을 거리입니다. 하지만, 장애물의 경계면을 넘으면서 저 거리를 이동하지 않았기때문에 추가적으로 거리를 빼 주어야 합니다.
이 거리는 어렵지 않게 구할 수 있습니다. sqrt(R * R - (R - h) * (R - h)) 이죠.
정리하면, 2 * R * arcos( (R - h) / R ) - 2 * sqrt(R * R - (R - h) * (R - h))로 식을 표현할 수 있습니다.
위의 과정을 정리한 것이 아래 소스코드입니다.
소스코드
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > SCPC' 카테고리의 다른 글
| [SCPC - 2018년 1차 예선] 우주정거장 (JAVA) (0) | 2020.08.19 |
|---|---|
| [SCPC - 2018년 1차 예선] 회문인 수의 합 (JAVA) (0) | 2020.08.19 |
| [SCPC - 2018년 1차 예선] 버스 타기 (JAVA) (0) | 2020.08.19 |
| [SCPC - 2019년 2차 예선] 소수 수열 (JAVA) (0) | 2020.08.18 |
| [SCPC - 2019년 1차 예선] 오르락 내리락 (JAVA) (0) | 2020.08.18 |



댓글