[BOJ] 백준 1238번 : 파티 (JAVA)
문제
N개의 숫자로 구분된 각각의 마을에 한 명의 학생이 살고 있다.
어느 날 이 N명의 학생이 X (1 ≤ X ≤ N)번 마을에 모여서 파티를 벌이기로 했다. 이 마을 사이에는 총 M개의 단방향 도로들이 있고 i번째 길을 지나는데 Ti(1 ≤ Ti ≤ 100)의 시간을 소비한다.
각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.
이 도로들은 단방향이기 때문에 아마 그들이 오고 가는 길이 다를지도 모른다. N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구일지 구하여라.
입력
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어온다. 시작점과 끝점이 같은 도로는 없으며, 시작점과 한 도시 A에서 다른 도시 B로 가는 도로의 개수는 최대 1개이다.
모든 학생들은 집에서 X에 갈수 있고, X에서 집으로 돌아올 수 있는 데이터만 입력으로 주어진다.
출력
첫 번째 줄에 N명의 학생들 중 오고 가는데 가장 오래 걸리는 학생의 소요시간을 출력한다.
풀이
다익스트라 알고리즘으로 해결할 수 있는 문제였습니다.
저는 처음에 입력을 그대로 받은 배열과 입력을 반대로 받은 배열에 대해서 플로이드 와샬 알고리즘을 수행한 뒤, arr[start][end] + arr[end][start]와 같이 N개의 정점에 대해서 거리를 더하는 로직을 세웠습니다.
(여기서 입력을 반대로 받았다는 의미는 "1 2 10" 대신 "2 1 10"을 받았다는 것을 뜻합니다.)
하지만, 플로이드 와샬 알고리즘은 O(N^3)이므로 N이 최대 1000인 조건에서는 사용하면 안 됩니다.
실제로 제가 이를 확인 안하고 제출했다가 시간 초과를 피할 수 없었죠.
그렇다면, 이를 어떻게 해결할 수 있을까요?
모든 정점에서 모든 정점에 대한 최단거리가 필요한 것이 아니라, 모든 정점에 대해서 X까지의 거리만 알면 됩니다.
따라서, 입력을 그대로 받은 배열에 대해서 X를 시작점으로 잡고 다익스트라 알고리즘을 수행한 후, 입력을 반대로 받은 배열에 대해서 X를 시작점으로 잡고 다익스트라 알고리즘을 수행하면 됩니다.
문제의 예시를 보면서 자세히 설명해 보겠습니다.
예시
문제의 입력을 그대로 받은 그래프는 아래와 같은 형태일 것입니다.
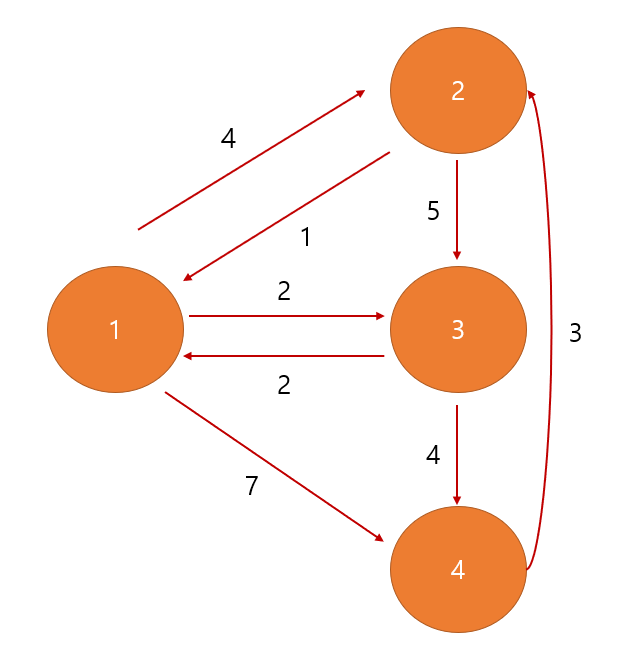
문제의 예시에서 X는 2이고, 2를 제외한 나머지 정점에서 X를 왕복하는 거리를 구해야합니다.
먼저, 우리는 위 그래프를 가지고 X에서 모든 정점에 대한 최단거리를 다익스트라 알고리즘을 통해 구할 수 있습니다.
<X에서 모든 정점 사이의 최단 거리>
| 1 | 2 | 3 | 4 |
| 1 | 0 | 3 | 7 |
이제, 모든 정점에서 X로 가는 최단 거리를 구해야 합니다.
여기서도 출발점을 X로 잡고 다익스트라 알고리즘을 수행해야 편하게 값을 구할 수 있습니다.
이를 수행하기 위하여 입력을 반대로 받은 배열을 정의해야합니다.
그리고 입력을 반대로 받은 그래프는 아래와 같은 형태일 것입니다.
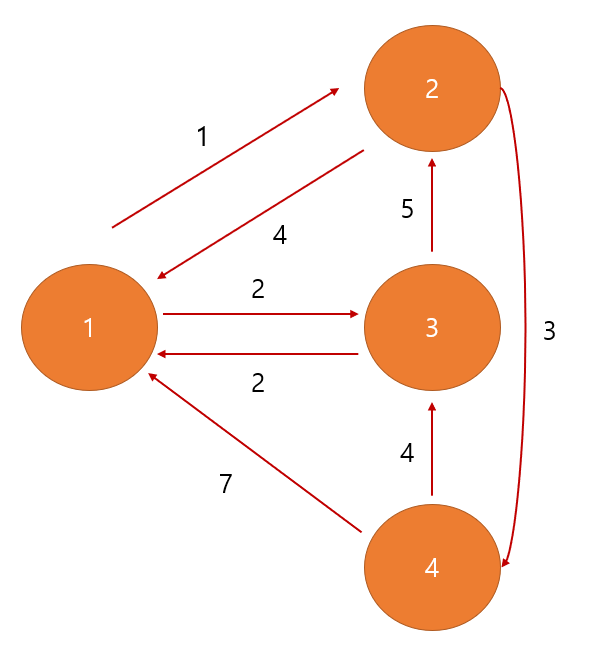
이제, 위 그래프를 가지고 모든 정점에 대해서 X로 가는 최단 거리를 구할 수 있습니다.
<X에서 모든 정점 사이의 최단 거리>
| 1 | 2 | 3 | 4 |
| 4 | 0 | 6 | 3 |
이제 할 일은 위 두 가지 표의 값을 이용하여 왕복 시간이 가장 오래 걸리는 시간을 출력하는 것입니다.
아래는 위 과정을 정리한 소스코드입니다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
|
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
class Town implements Comparable<Town> {
int end;
int weight;
Town(int end, int weight) {
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Town arg0) {
return weight - arg0.weight;
}
}
public class Main {
static final int INF = 987654321;
static ArrayList<ArrayList<Town>> arrList, reverse_arrList;
static int N, X;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
X = Integer.parseInt(st.nextToken());
arrList = new ArrayList<>(); // 문제의 입력을 그대로 받은 배열
reverse_arrList = new ArrayList<>(); // 문제의 입력을 반대로 받은 배열
for (int i = 0; i <= N; i++) {
arrList.add(new ArrayList<>());
reverse_arrList.add(new ArrayList<>());
}
// arrList와 reverse_arrList를 각각 단방향 인접리스트로 구현
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
arrList.get(start).add(new Town(end, weight));
reverse_arrList.get(end).add(new Town(start, weight));
}
int[] dist1 = dijkstra(arrList); // X에서 시작점들 사이의 최단거리
int[] dist2 = dijkstra(reverse_arrList); // 시작점들에서 X 사이의 최단거리
int ans = 0;
for (int i = 1; i <= N; i++) {
ans = Math.max(ans, dist1[i] + dist2[i]);
}
bw.write(ans + "\n");
bw.flush();
bw.close();
br.close();
}
// 다익스트라 알고리즘
public static int[] dijkstra(ArrayList<ArrayList<Town>> a) {
PriorityQueue<Town> pq = new PriorityQueue<>();
pq.offer(new Town(X, 0));
boolean[] check = new boolean[N + 1];
int[] dist = new int[N + 1];
Arrays.fill(dist, INF);
dist[X] = 0;
while (!pq.isEmpty()) {
Town curTown = pq.poll();
int cur = curTown.end;
if (!check[cur]) {
check[cur] = true;
for (Town town : a.get(cur)) {
if (!check[town.end] && dist[town.end] > dist[cur] + town.weight) {
dist[town.end] = dist[cur] + town.weight;
pq.add(new Town(town.end, dist[town.end]));
}
}
}
}
return dist;
}
}
|
cs |
지적 혹은 조언 환영합니다! 언제든지 댓글로 남겨주세요.
'PS > 백준' 카테고리의 다른 글
| [BOJ] 백준 1717번 : 집합의 표현 (JAVA) (0) | 2020.08.04 |
|---|---|
| [BOJ] 백준 1602번 : 도망자 원숭이 (JAVA) (0) | 2020.08.03 |
| [BOJ] 백준 1507번 : 궁금한 민호 (JAVA) (0) | 2020.08.03 |
| [BOJ] 백준 2610번 : 회의준비 (JAVA) (0) | 2020.08.03 |
| [BOJ] 백준 11562번 : 백양로 브레이크 (JAVA) (1) | 2020.08.02 |



댓글